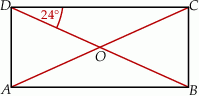
Oblicz miarę kąta ostrego, pod którym przecinają się przekątne prostokąta przedstawionego na rysunku.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz miarę kąta ostrego, pod którym przecinają się przekątne prostokąta przedstawionego na rysunku.

Oblicz miarę kąta ostrego, pod którym przecinają się przekątne prostokąta przedstawionego na rysunku.
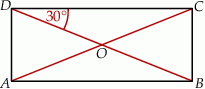
Oblicz miarę kąta ostrego, pod którym przecinają się przekątne prostokąta przedstawionego na rysunku.
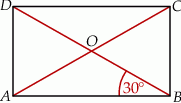
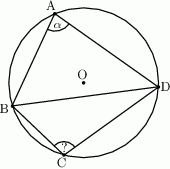
Wszystkie wierzchołki czworokąta 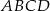 leżą na okręgu oraz
leżą na okręgu oraz 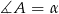 . Oblicz miarę kąta
. Oblicz miarę kąta 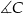 .
.
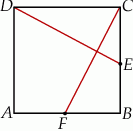
Na rysunku przedstawiono kwadrat 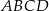 . Punkty
. Punkty 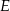 i
i 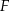 są środkami boków
są środkami boków 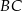 i
i 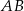 . Uzasadnij, że odcinki
. Uzasadnij, że odcinki 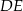 i
i 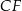 są prostopadłe.
są prostopadłe.
Krótsza podstawa trapezu ma długość 2, a ramiona długości 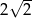 i 4 tworzą z dłuższą podstawą kąty o miarach
i 4 tworzą z dłuższą podstawą kąty o miarach 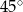 i
i 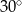 . Oblicz pole trapezu.
. Oblicz pole trapezu.
Krótsza podstawa trapezu ma długość 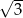 , a ramiona długości
, a ramiona długości 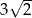 i 6 tworzą z dłuższą podstawą kąty o miarach
i 6 tworzą z dłuższą podstawą kąty o miarach 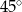 i
i 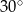 odpowiednio. Oblicz pole trapezu.
odpowiednio. Oblicz pole trapezu.
Przekątna prostokąta 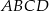 nachylona jest do jednego z jego boków pod kątem
nachylona jest do jednego z jego boków pod kątem 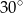 . Uzasadnij, że pole prostokąta
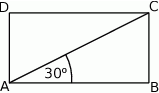
. Uzasadnij, że pole prostokąta 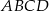 jest równe polu trójkąta równobocznego o boku równym przekątnej tego prostokąta.
jest równe polu trójkąta równobocznego o boku równym przekątnej tego prostokąta.
Przekątna prostokąta 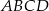 nachylona jest do jednego z jego boków pod kątem
nachylona jest do jednego z jego boków pod kątem 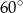 . Uzasadnij, że pole prostokąta
. Uzasadnij, że pole prostokąta 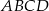 jest równe polu trójkąta równobocznego o boku równym przekątnej tego prostokąta.
jest równe polu trójkąta równobocznego o boku równym przekątnej tego prostokąta.
Dany jest romb 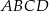 . Obwód tego rombu jest równy 52 cm, a przekątna
. Obwód tego rombu jest równy 52 cm, a przekątna 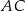 ma długość 24 cm (zobacz rysunek poniżej).
ma długość 24 cm (zobacz rysunek poniżej).
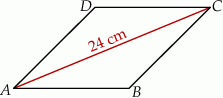
Oblicz długość przekątnej 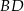 rombu
rombu 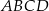 .
.
Dany jest romb 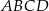 . Obwód tego rombu jest równy 68 cm, a przekątna
. Obwód tego rombu jest równy 68 cm, a przekątna 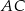 ma długość 30 cm (zobacz rysunek poniżej).
ma długość 30 cm (zobacz rysunek poniżej).
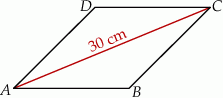
Oblicz długość przekątnej 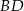 rombu
rombu 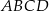 .
.
Wykaż, że w dowolnym trapezie suma długości podstaw jest mniejsza od sumy długości przekątnych.
Wykaż, że w dowolnym trapezie suma długości ramion jest mniejsza od sumy długości przekątnych.
Obwód trapezu równoramiennego wynosi 32 cm. Wysokość poprowadzona z wierzchołka kąta rozwartego dzieli podstawę na dwa odcinki o długościach 3 cm i 11 cm. Oblicz pole trapezu.
Obwód trapezu równoramiennego wynosi 50 cm. Wysokość poprowadzona z wierzchołka kąta rozwartego dzieli podstawę na dwa odcinki o długościach 5 cm i 12 cm. Oblicz pole trapezu.
Na rysunku przedstawiono prostokąt 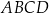 , w którym bok
, w którym bok 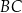 ma długość 4 cm. Na bokach prostokąta zaznaczono punkty
ma długość 4 cm. Na bokach prostokąta zaznaczono punkty 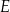 i
i 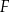 oraz narysowano odcinki
oraz narysowano odcinki 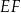 i
i 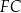 tak, że powstały dwa jednakowe trójkąty
tak, że powstały dwa jednakowe trójkąty 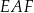 i
i 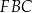 . W obu trójkątach zaznaczono kąty o takiej samej mierze
. W obu trójkątach zaznaczono kąty o takiej samej mierze  . Odcinek
. Odcinek 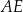 ma długość 3 cm.
ma długość 3 cm.
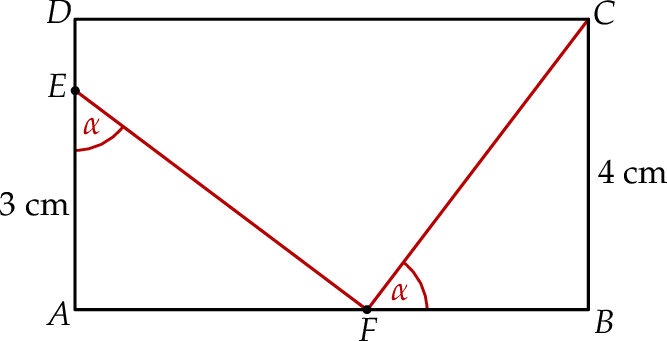
Oblicz pole prostokąta 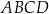 .
.
Oblicz pole i obwód równoległoboku przedstawionego na rysunku.
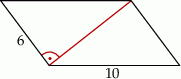
Oblicz pole i obwód równoległoboku przedstawionego na rysunku.
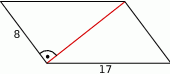
Oblicz pole i obwód równoległoboku przedstawionego na rysunku.
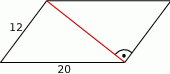
Obwód trapezu równoramiennego jest równy 72 cm, ramię ma długość 20 cm, a różnica długości podstaw wynosi 24 cm. Oblicz pole tego trapezu. Zapisz obliczenia.
Obwód trapezu równoramiennego jest równy 56 cm, ramię ma długość 15 cm, a różnica długości podstaw wynosi 18 cm. Oblicz pole tego trapezu. Zapisz obliczenia.
Jeden z boków równoległoboku jest o 2,5 cm krótszy od drugiego boku. Obwód tego równoległoboku jest równy 29 cm. Oblicz długości jego boków.
Czworokąty 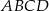 i
i 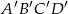 są podobne. Boki czworokąta
są podobne. Boki czworokąta 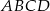 mają długości 8 cm, 4 cm, 16 cm, 12 cm. Najdłuższy bok czworokąta
mają długości 8 cm, 4 cm, 16 cm, 12 cm. Najdłuższy bok czworokąta 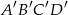 ma 20 cm. Jakie są długości pozostałych boków?
ma 20 cm. Jakie są długości pozostałych boków?
Długości boków czworokąta opisano za pomocą wyrażeń algebraicznych, tak jak pokazano na rysunku.
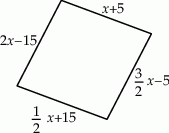
Uzasadnij, że jeśli obwód tego czworokąta jest równy 100 cm, to jest on rombem.
Wykaż, że jeżeli każda przekątna czworokąta wypukłego dzieli go na trójkąty o równych polach to czworokąt ten jest równoległobokiem.
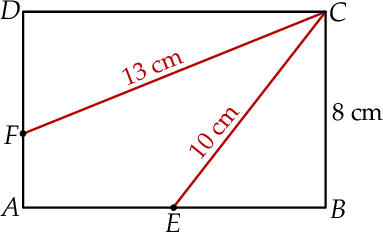
W prostokącie 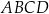 o polu
o polu 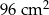 bok
bok 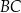 ma długość 8 cm. Na bokach
ma długość 8 cm. Na bokach 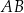 i
i 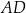 wybrano punkty
wybrano punkty 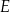 i
i 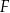 tak, że
tak, że 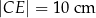 i
i 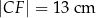 . Oblicz pole czworokąta
. Oblicz pole czworokąta  .
.
Z dwóch przeciwległych wierzchołków kwadratu o boku 2 zakreślono okręgi o promieniu 2. Oblicz pole „soczewki” wyznaczonej przez te okręgi.
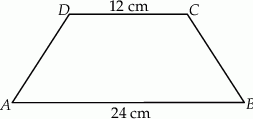
Podstawy trapezu równoramiennego  mają długości: 12 cm i 24 cm. Pole tego trapezu jest równe
mają długości: 12 cm i 24 cm. Pole tego trapezu jest równe 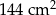 . Oblicz obwód trapezu
. Oblicz obwód trapezu  .
.
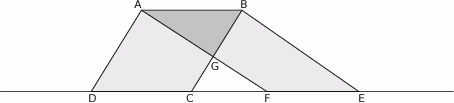
Na rysunku przedstawiono dwa równoległoboki  i
i  . Uzasadnij, że czworokąty
. Uzasadnij, że czworokąty 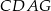 oraz
oraz 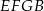 mają równe pola.
mają równe pola.
Oblicz długości boków prostokąta o obwodzie 1,1 dm którego boki są proporcjonalne do odcinków długości 4 cm i 7 cm.
