/Szkoła podstawowa/Geometria/Czworokąty

Zadanie nr 1503205

Dodaj do ulubionych
Dodaj do rozwiązanych

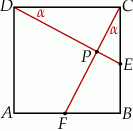
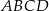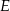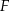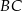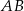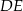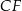Na rysunku przedstawiono kwadrat ABCD . Punkty E i F są środkami boków BC i AB . Uzasadnij, że odcinki DE i CF są prostopadłe.

PIC

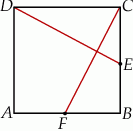
Rozwiązanie

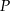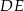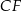Niech P będzie punktem wspólnym odcinków DE i CF oraz niech ∡EDC = α .

PIC

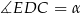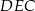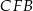Zauważmy, że trójkąty prostokątne DEC i CF B są przystające, więc

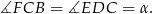
∡F CB = ∡EDC = α.

Teraz łatwo już obliczyć miarę kąta 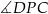∡DP C .

∘ ∘ ∘ ∡DP C = 1 80 − ∡P DC − ∡P CD = 180 − α − (9 0 − ∡P CE ) = = 1 80∘ − α− (90∘ − α) = 18 0∘ − α− 90∘ + α = 90∘.
Wersja PDF