Zadanie nr 4111372

Rozwiąż nierówność 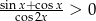sinx+cosx cos2x > 0 , gdzie x ∈ ⟨0;2π ⟩ .

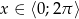Rozwiązanie

Aby podana nierówność miała sens musi być

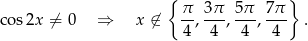
{ π 3π 5π 7π } cos 2x ⁄= 0 ⇒ x ⁄∈ --,---,---,--- . 4 4 4 4

Przekształcamy podaną nierówność.

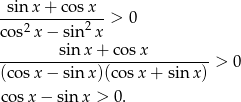
sin x + cos x ---------------> 0 cos2x − sin2x --------sin-x-+-cos-x--------- (cosx − sin x)(cosx + sin x) > 0 cosx − sin x > 0.

Skorzystamy teraz ze wzoru na cosinus sumy:

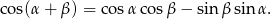
co s(α+ β) = cos αco sβ − sin βsin α.

Mamy zatem

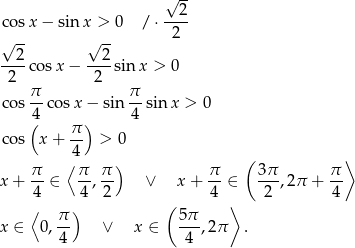
√ -- cos x− sin x > 0 / ⋅--2- √ -- √ -- 2 2 2 ----cosx − ----sin x > 0 2 π 2 π cos --cos x− sin -- sin x > 0 4( ) 4 cos x + π- > 0 4 ( ⟩ π- ⟨π- π-) π- 3π- π- x+ 4 ∈ 4, 2 ∨ x + 4 ∈ 2 ,2π + 4 ⟨ ) ( ⟩ x ∈ 0, π- ∨ x ∈ 5π-,2π . 4 4

Wypisując powyższe przedziały, uwzględnialiśmy warunek 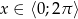x ∈ ⟨0 ;2π⟩ . Jeżeli przypomnimy sobie dziedzinę nierówności, to mamy

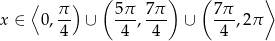
( ) ( ⟩ ⟨ π ) 5π 7π 7π x ∈ 0,4- ∪ -4-,-4- ∪ -4-,2π

Odpowiedź: ⟨ π) (5π 7π) (7π ⟩ x ∈ 0 ,4- ∪ -4-,4-- ∪ -4 ,2π