/Szkoła średnia/Nierówności/Trygonometryczne/Rozwiąż nierówność

Zadanie nr 9605537

Dodaj do ulubionych
Dodaj do rozwiązanych

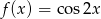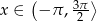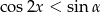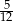Posługując się wykresem funkcji f(x) = co s2x dla ( 3π⟩ x ∈ − π , 2 , rozwiąż nierówność cos 2x < sin α wiedząc, że miara kąta α jest równa mierze łukowej kąta środkowego okręgu opartego na 512 okręgu.

Rozwiązanie

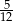Obliczmy najpierw α – jest to 5- 12 kąta pełnego, czyli

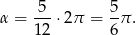
5 5 α = ---⋅2 π = -π . 12 6

Zatem

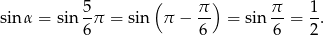
5 ( π ) π 1 sin α = sin 6-π = sin π − 6- = sin 6-= 2-.

Teraz szkicujemy wykres 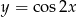y = cos 2x .

PIC

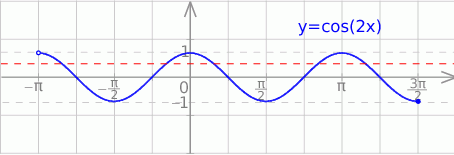
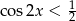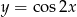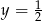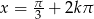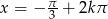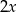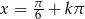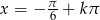Rozwiązanie nierówności cos2x < 12 odczytamy z wykresu, ale najpierw zastanówmy się, gdzie funkcja y = cos 2x przecina prostą y = 1 2 . Zwykły cosinus przecina tę prostą w punktach x = π-+ 2kπ 3 i x = − π-+ 2k π 3 . My mamy jednak 2x zamiast x , co daje nam punkty π- x = 6 + kπ i π x = − 6-+ kπ . Łatwo sprawdzić, że w interesującym nas przedziale jest 5 punktów tej postaci:

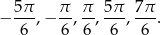
− 5π-,− π-, π-, 5π-, 7-π . 6 6 6 6 6

Teraz z obrazka odczytujemy rozwiązanie nierówności:

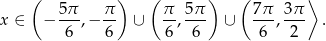
( ) ( ) ( ⟩ x ∈ − 5π-,− π- ∪ π-, 5π ∪ 7π-, 3π- . 6 6 6 6 6 2

 
Odpowiedź: ( ) ( ) ( ⟩ − 5π,− π- ∪ π, 5π ∪ 7π-, 3π 6 6 6 6 6 2

Wersja PDF