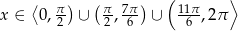Zadanie nr 9853361
Rozwiąż nierówność 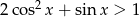 , gdzie
, gdzie 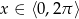 .
.
Rozwiązanie
Przekształcamy nierówność tak, aby móc podstawić 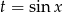 .
.
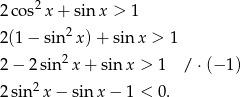
Podstawiamy teraz 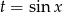 .
.
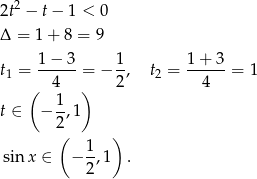
Teraz szkicujemy sinus
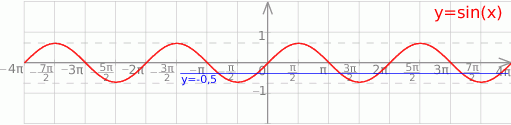
i odczytujemy zbiór rozwiązań nierówności:
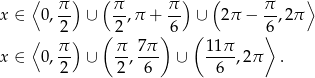
Odpowiedź: 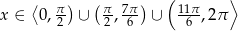
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż nierówność 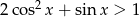 , gdzie
, gdzie 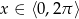 .
.
Przekształcamy nierówność tak, aby móc podstawić 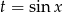 .
.
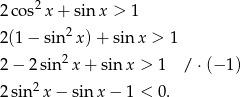
Podstawiamy teraz 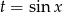 .
.
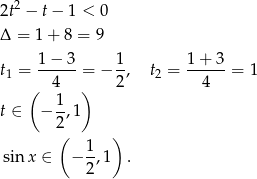
Teraz szkicujemy sinus

i odczytujemy zbiór rozwiązań nierówności:
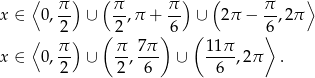
Odpowiedź: