/Szkoła średnia/Zadania maturalne/Matura 2012

Lubelska próba przed maturą
z matematyki (dla klas trzecich)
poziom rozszerzony 15 luty 2012 Czas pracy: 180 minut

Zadanie 1
(5 pkt)

Dla jakich wartości parametru 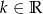k ∈ R zbiory

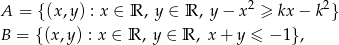
A = {(x,y) : x ∈ R, y ∈ R , y − x 2 ≥ kx− k2} B = { (x,y) : x ∈ R , y ∈ R , x + y ≤ − 1} ,

są rozłączne?

Zadanie 2
(4 pkt)

Rozwiąż nierówność 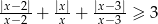|x−2| |x| |x−3| -x−2-+ -x-+ -x−3-≥ 3 .

Zadanie 3
(4 pkt)

Wyznacz dziedzinę funkcji określonej wzorem 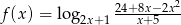2 f(x) = log2x+ 1 24+8xx+−5-2x .

Zadanie 4
(4 pkt)

Ciąg 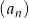(an) jest ciągiem geometrycznym. Wykaz, że ciąg 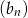(bn ) określony wzorem 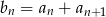bn = an + an+ 1 jest również ciągiem geometrycznym.

Zadanie 5
(4 pkt)

Wykazać, że 1 nie jest wyrazem ciągu 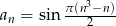a = sin π-(n3−n) n 2 .

Zadanie 6
(4 pkt)

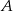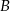Dziesięć osób rozdzielono na dwie drużyny po 5 osób. Oblicz prawdopodobieństwo, że osoby A i B będą w przeciwnych drużynach.

Zadanie 7
(5 pkt)

Zaznacz w układzie współrzędnych zbiór wszystkich par 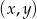(x,y ) liczb rzeczywistych, dla których wyrażenie: 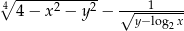∘ ------------ 4 4− x2 − y2 − √---1---- y−log2x ma wartości rzeczywiste.

Zadanie 8
(3 pkt)

Wykaż, że jeżeli 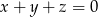x + y + z = 0 to zachodzi równość

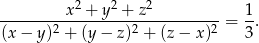
2 2 2 ---------x--+-y--+-z---------- = 1. (x − y )2 + (y − z)2 + (z − x)2 3

Zadanie 9
(5 pkt)

Wspólne styczne dwóch okręgów stycznych zewnętrznie przecinają się pod kątem 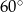60∘ . Wyznacz stosunek długości promieni tych okręgów.

Zadanie 10
(6 pkt)

Dane są punkty 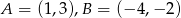A = (1,3),B = (− 4,− 2) . Wyznacz taki punkt 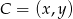C = (x,y) , gdzie 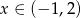x ∈ (− 1,2) leżący na paraboli o równaniu 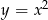y = x2 , aby pole trójkąta 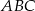ABC było największe.

Zadanie 11
(6 pkt)

Ściany boczne ostrosłupa prawidłowego trójkątnego są trójkątami o przyprostokątnych długości 12 cm. Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.

Arkusz Wersja PDF
Rozwiązania