/Szkoła średnia/Zadania maturalne/Matura 2012

Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 21 kwietnia 2012 Czas pracy: 180 minut

Zadanie 1
(3 pkt)

Która liczba jest większa 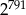791 2 , czy 339 5 ?

Zadanie 2
(5 pkt)

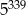Rozwiąż równanie 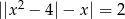||x2 − 4|− x | = 2 .

Zadanie 3
(3 pkt)

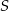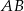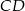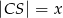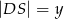Przez środek S cięciwy AB okręgu poprowadzono cięciwę CD , przy czym |CS | = x i |DS | = y . Oblicz długość cięciwy AB .

Zadanie 4
(5 pkt)

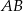Rozwiąż równanie 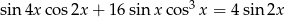sin 4x cos 2x+ 16sin xco s3x = 4 sin2x w przedziale ⟨0,2π ⟩ .

Zadanie 5
(3 pkt)

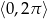Uzasadnij, że jeżeli 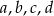a,b,c,d są liczbami dodatnimi to

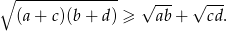
∘ -------------- √ --- √ --- (a+ c)(b+ d ) ≥ ab+ cd.

Zadanie 6
(5 pkt)

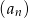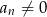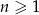Wyrazy ciągu geometrycznego (an) , w którym an ⁄= 0 dla n ≥ 1 spełniają warunek

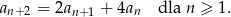
an+ 2 = 2an+1 + 4an dla n ≥ 1.

Wykaż, że wyrazy tego ciągu spełniają również warunek

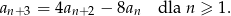
an+ 3 = 4an+2 − 8an dla n ≥ 1.

Zadanie 7
(6 pkt)

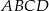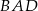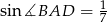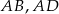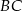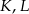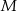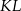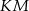Dany jest romb ABCD o boku długości 1, w którym kąt BAD jest ostry i sin ∡BAD = 17 . Na bokach AB ,AD i BC wybrano odpowiednio punkty K,L i M w ten sposób, że odcinki KL i KM są równoległe do przekątnych rombu.

  • Oblicz pole czworokąta CDLM .
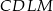  • Oblicz największą możliwą wartość pola trójkąta KLM .

Zadanie 8
(4 pkt)

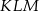Wykaż, że dla dowolnych punktów płaszczyzny 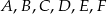A ,B,C ,D ,E,F spełniona jest równość.

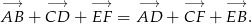
−→ −→ −→ −→ −→ −→ AB + CD + EF = AD + CF + EB .

Zadanie 9
(5 pkt)

Okrąg wpisany w trójkąt 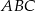ABC ma równanie 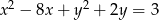2 2 x − 8x + y + 2y = 3 . Oblicz 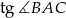tg ∡BAC jeżeli A = (− 4,− 7) .

Zadanie 10
(6 pkt)

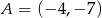Ostrosłup prawidłowy trójkątny przecięto płaszczyzną przechodzącą przez krawędź podstawy długości a i środek wysokości ostrosłupa. Płaszczyzna ta jest nachylona do płaszczyzny podstawy pod kątem α . Oblicz objętość i pole powierzchni bocznej ostrosłupa.

Zadanie 11
(5 pkt)

Liczby ze zbioru 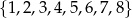{1 ,2,3,4,5,6,7,8} ustawiamy w przypadkowej kolejności (bez powtórzeń) tworząc liczbę ośmiocyfrową. Jakie jest prawdopodobieństwo otrzymania liczby, w której jednocześnie:
– cyfra 1 stoi na lewo od cyfry 2,
– cyfra 3 stoi na lewo od cyfry 4,
– cyfra 5 stoi na lewo od cyfry 6,
– cyfra 7 stoi na lewo od cyfry 8?
Uwaga, w powyższych warunkach nie zakładamy, że odpowiednie cyfry stoją obok siebie, np. liczba 13275846 spełnia wszystkie powyższe warunki.

Arkusz Wersja PDF
Rozwiązania