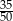Wyrażenie 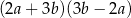 jest równe
jest równe
A) 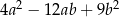 B)
B) 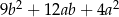 C)
C) 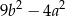 D)
D) 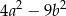
/Szkoła podstawowa/Zadania testowe
Wyrażenie 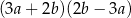 jest równe
jest równe
A) 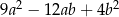 B)
B) 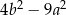 C)
C) 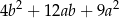 D)
D) 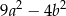
Długość każdego boku kwadratu zwiększono o 20%. Wtedy pole tego kwadratu:
A) wzrośnie o 20% B) wzrośnie o 40% C) wzrośnie o 44% D) wzrośnie dwukrotnie
Długość boku kwadratu 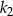 jest o 10% większa od długości boku kwadratu
jest o 10% większa od długości boku kwadratu 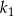 . Wówczas pole kwadratu
. Wówczas pole kwadratu 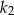 jest większe od pola kwadratu
jest większe od pola kwadratu 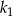 o
o
A) 10% B) 110% C) 21% D) 121%
Przekątna 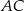 prostokąta
prostokąta 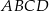 ma długość 70. Na boku
ma długość 70. Na boku 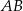 obrano punkt
obrano punkt 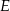 , na przekątnej
, na przekątnej 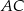 obrano punkt
obrano punkt 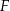 , a na boku
, a na boku 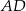 obrano punkt
obrano punkt 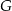 – tak, że czworokąt
– tak, że czworokąt 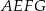 jest prostokątem (zobacz rysunek). Ponadto
jest prostokątem (zobacz rysunek). Ponadto 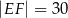 i
i 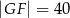 .
.
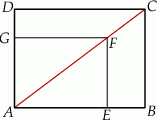
Obwód prostokąta 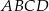 jest równy
jest równy
A) 158 B) 196 C) 336 D) 490
Przekątna 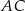 prostokąta
prostokąta 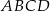 ma długość 104. Na boku
ma długość 104. Na boku 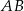 obrano punkt
obrano punkt 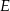 , na przekątnej
, na przekątnej 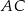 obrano punkt
obrano punkt 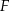 , a na boku
, a na boku 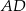 obrano punkt
obrano punkt 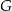 – tak, że czworokąt
– tak, że czworokąt 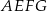 jest prostokątem (zobacz rysunek). Ponadto
jest prostokątem (zobacz rysunek). Ponadto 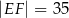 i
i 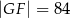 .
.
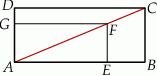
Obwód prostokąta 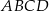 jest równy
jest równy
A) 272 B) 238 C) 221 D) 136
Uczeń przeczytał w ciągu tygodnia książkę liczącą 420 stron.
| Dzień | Liczba przeczytanych stron | Czas czytania |
| 1. | 50 | 1 h 40 min |
| 2. | 70 | 2 h |
| 3. | 90 | 2 h 20 min |
| 4. | 30 | 30 min |
| 5. | 70 | 2 h 10 min |
| 6. | 80 | 2 h 30 min |
| 7. | 30 | 30 min |
Na podstawie informacji zawartych w powyższej tabeli wybierz zdanie prawdziwe.
A) Pierwszego dnia uczeń przeczytał ponad 20% całej książki.
B) Uczeń czytał średnio 50 stron dziennie.
C) Piątego dnia uczeń przeczytał 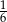 całej książki.
całej książki.
D) Przeczytanie pierwszej połowy książki zajęło uczniowi mniej czasu niż przeczytanie drugiej połowy.
Dany jest trapez 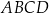 , w którym przekątna
, w którym przekątna 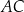 jest prostopadła do ramienia
jest prostopadła do ramienia 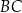 ,
, 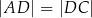 oraz
oraz 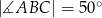 (zobacz rysunek).
(zobacz rysunek).
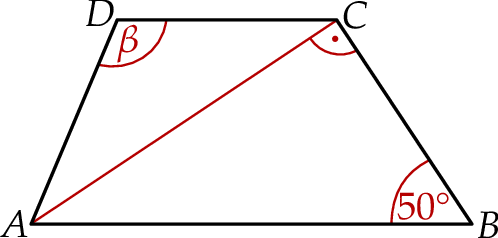
Stąd wynika, że
A) 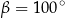 B)
B) 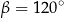 C)
C) 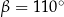 D)
D) 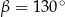
Dany jest trapez 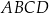 , w którym bok
, w którym bok 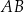 jest równoległy do boku
jest równoległy do boku 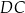 . W tym trapezie poprowadzono odcinek
. W tym trapezie poprowadzono odcinek 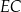 równoległy do boku
równoległy do boku 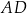 , podano miary dwóch kątów oraz oznaczono kąt
, podano miary dwóch kątów oraz oznaczono kąt  (zobacz rysunek).
(zobacz rysunek).

Kąt  ma miarę
ma miarę
A) 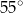 B)
B) 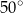 C)
C) 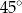 D)
D) 
Dany jest trapez 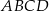 , w którym przekątna
, w którym przekątna 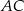 jest prostopadła do ramienia
jest prostopadła do ramienia 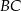 ,
, 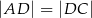 oraz
oraz 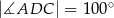 (zobacz rysunek).
(zobacz rysunek).
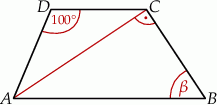
Stąd wynika, że
A) 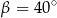 B)
B) 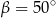 C)
C) 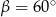 D)
D) 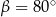
Na rysunku przedstawiono bryłę zbudowaną z sześciu jednakowych sześcianów. Objętość tej bryły jest równa 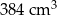 .
.
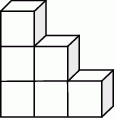
Pole powierzchni całkowitej tej bryły jest równe
A) 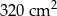 B)
B) 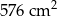 C)
C) 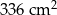 D)
D) 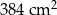
Na rysunku przedstawiono bryłę zbudowaną z sześciu jednakowych sześcianów. Objętość tej bryły jest równa 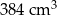 .
.
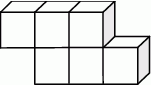
Pole powierzchni całkowitej tej bryły jest równe
A) 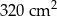 B)
B) 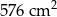 C)
C) 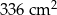 D)
D) 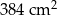
Ula w trakcie loterii charytatywnej sprzedawała dwa rodzaje losów: losy za 5 złotych i losy za 7 złotych. W sumie sprzedała 92 losy, przy czym sprzedała 3 razy więcej losów za 5 zł, niż losów za 7 złotych. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Liczba sprzedanych losów za 5 złotych była o 46 większa od liczby sprzedanych losów za 7 złotych. | P | F |
| Wartość sprzedanych losów wyniosła: 500 zł. | P | F |
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Liczba 1725 jest liczbą podzielną przez 15. | P | F |
| Liczba 1725 jest wielokrotnością 125. | P | F |
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Liczba 81390 jest liczbą podzielną przez 60. | P | F |
| Liczba 46125 jest wielokrotnością 375. | P | F |
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Liczba 3480 jest liczbą podzielną przez 45. | P | F |
| Liczba 3480 jest wielokrotnością 16. | P | F |
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Liczba 16848 jest liczbą podzielną przez 32. | P | F |
| Liczba 16848 jest wielokrotnością 81. | P | F |
W szkole Adama w gazetce szkolnej ukazał się artykuł, dotyczący wyboru przez ósmoklasistów szkoły ponadpodstawowej.
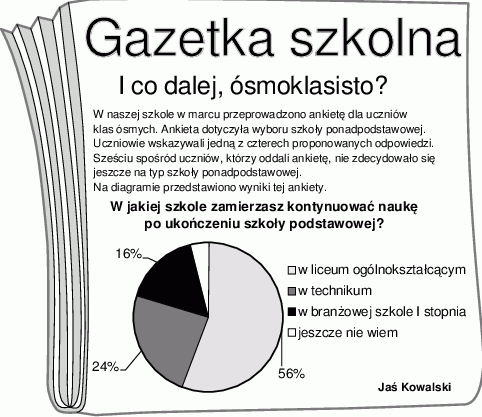
Poniżej zapisano trzy prawdziwe informacje.
I. Ankietę oddało łącznie 150 uczniów.
II. W ankiecie wzięli udział wszyscy uczniowie klas ósmych.
III. Łącznie mniej niż połowa uczniów biorących udział w ankiecie zamierza kontynuować naukę w technikum lub w branżowej szkole.
Które z informacji – I, II, III – wynikają z analizy danych zamieszczonych w treści artykułu?
A) Tylko I i II. B) Tylko I i III. C) Tylko II i III. D) Wszystkie – I, II i III.
W szkole Adama w gazetce szkolnej ukazał się artykuł, dotyczący wyboru przez ósmoklasistów szkoły ponadpodstawowej.
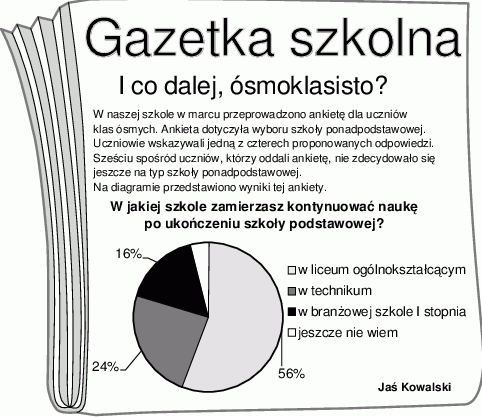
Poniżej zapisano trzy informacje.
I. Ankietę oddało łącznie 120 uczniów.
II. Ponad 80 spośród ankietowanych osób zamierza kontynuować naukę w liceum.
III. Łącznie mniej niż połowa uczniów biorących udział w ankiecie zamierza kontynuować naukę w technikum lub w branżowej szkole.
Które z informacji – I, II, III – wynikają z analizy danych zamieszczonych w treści artykułu?
A) Tylko I i II. B) Tylko I i III. C) Tylko II i III. D) Wszystkie – I, II i III.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Jeżeli średnicę podstawy stożka zwiększymy 3 razy, a jego wysokość zmniejszymy 3 razy, to objętość stożka
A) zwiększy się dziewięciokrotnie. B) zmniejszy się trzykrotnie.
C) zwiększy się trzykrotnie. D) nie zmieni się.
Ze zbioru kolejnych liczb naturalnych 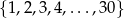 losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest kwadratem liczby całkowitej, jest równe
losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest kwadratem liczby całkowitej, jest równe
A) 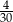 B)
B) 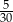 C)
C) 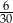 D)
D) 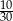
Ze zbioru kolejnych liczb naturalnych 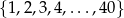 losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest kwadratem liczby całkowitej, jest równe
losujemy jedną liczbę. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest kwadratem liczby całkowitej, jest równe
A) 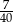 B)
B) 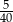 C)
C) 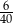 D)
D) 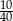
Ze zbioru kolejnych liczb naturalnych 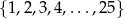 losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby, która jest kwadratem liczby całkowitej, jest równe
losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby, która jest kwadratem liczby całkowitej, jest równe
A) 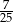 B)
B) 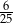 C)
C) 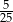 D)
D) 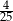
W tabeli zapisano cztery liczby.
| I | 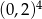 |
| II | 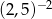 |
| III | 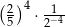 |
| IV | 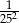 |
Liczba 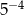 jest równa liczbom
jest równa liczbom
A) I i II B) I i IV C) II i IV D) II i III
Wartość wyrażenia 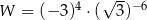 pomnożono przez 2. Wartość tego wyrażenia
pomnożono przez 2. Wartość tego wyrażenia
A) zmniejszyła się o 3 B) zwiększyła się o 3
C) zmniejszyła się o 2 D) zwiększyła się o 2
Wartość wyrażenia 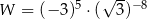 pomnożono przez 3. Wartość tego wyrażenia
pomnożono przez 3. Wartość tego wyrażenia
A) zwiększyła się o 6 B) zwiększyła się o 3
C) zmniejszyła się o 6 D) zwiększyła się o 9
Wartość wyrażenia 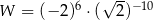 pomnożono przez 2. Wartość tego wyrażenia
pomnożono przez 2. Wartość tego wyrażenia
A) zmniejszyła się o 4 B) zwiększyła się o 4
C) zmniejszyła się o 2 D) zwiększyła się o 2
Funkcja 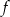 przyporządkowuje każdej liczbie naturalnej większej od 1 liczbę liczb pierwszych mniejszych od
przyporządkowuje każdej liczbie naturalnej większej od 1 liczbę liczb pierwszych mniejszych od  . Liczba
. Liczba 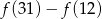 jest równa
jest równa
A) 5 B) 6 C) 4 D) 10
Podczas suszenia grzyby tracą 80% swojej masy. Ile ważą po wysuszeniu 2 kilogramy grzybów?
A) 0,20 kg B) 0,24 kg C) 0,4 kg D) 0,96 kg
Podczas suszenia grzyby tracą 80% swojej masy. Ile waży po wysuszeniu 1 kg grzybów?
A) 0,20 kg B) 0,24 kg C) 0,4 kg D) 0,96 kg
Podczas suszenia grzyby tracą 80% swojej masy. Ile waży po wysuszeniu 2,4 kg grzybów?
A) 0,40 kg B) 0,48 kg C) 0,8 kg D) 0,96 kg
Dane są liczby: 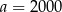 ,
, 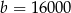 ,
, 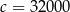 . Wartość wyrażenia
. Wartość wyrażenia 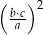 jest równa
jest równa
A) 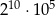 B)
B) 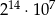 C)
C) 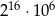 D)
D) 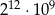
Pary liczb 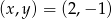 i
i 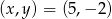 należą do zbioru rozwiązań układu równań
należą do zbioru rozwiązań układu równań
A) 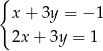 B)
B) 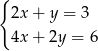 C)
C) 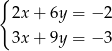 D)
D) 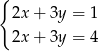
Pary liczb 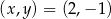 i
i 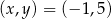 należą do zbioru rozwiązań układu równań
należą do zbioru rozwiązań układu równań
A) 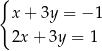 B)
B) 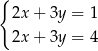 C)
C) 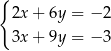 D)
D) 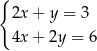
Do napełniania basenu służą dwa zawory. Jeżeli oba zawory są odkręcone jednocześnie, to basen napełnia się w ciągu 30 minut. Jeżeli odkręcony jest wyłącznie pierwszy zawór, to basen napełnia się w ciągu 66 minut. Jeżeli odkręcony jest wyłącznie drugi zawór, to basen napełnia się w ciągu A/B minut.
A) 60 B) 55
Objętość wody, która przepłynie przez zawór pierwszy w ciągu 6 minut jest taka sama jak objętość wody, która przepłynie przez zawór drugi w ciągu C/D minut.
C) 4 D) 5
Dane są liczby: 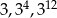 . Iloczyn tych liczb jest równy
. Iloczyn tych liczb jest równy
A) 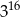 B)
B) 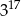 C)
C) 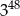 D)
D) 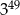
Dane są liczby: 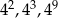 . Iloczyn tych liczb jest równy
. Iloczyn tych liczb jest równy
A) 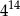 B)
B) 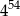 C)
C) 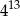 D)
D) 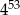
Na loterii jest 10 losów, z których 4 są wygrywające. Kupujemy jeden los. Prawdopodobieństwo zdarzenia, że nie wygramy nagrody, jest równe
A)  B)
B)  C)
C)  D)
D) 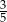
Na loterii jest 14 losów, z których 6 jest wygrywających. Kupujemy jeden los. Prawdopodobieństwo zdarzenia, że nie wygramy nagrody jest równe
A)  B)
B)  C)
C) 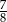 D)
D) 
Na loterii jest 20 losów, z których 8 jest wygrywających. Kupujemy jeden los. Prawdopodobieństwo zdarzenia, że nie wygramy nagrody jest równe
A) 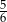 B)
B) 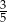 C)
C) 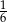 D)
D) 
Na loterii jest 12 losów, z których 8 jest przegrywających. Kupujemy jeden los. Prawdopodobieństwo zdarzenia, że wygramy nagrodę jest równe
A) 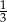 B)
B) 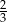 C)
C) 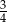 D)
D) 
W pudełku jest 50 kuponów, wśród których jest 15 kuponów przegrywających, a pozostałe kupony są wygrywające. Z tego pudełka w sposób losowy wyciągamy jeden kupon. Prawdopodobieństwo zdarzenia polegającego na tym, że wyciągniemy kupon wygrywający, jest równe
A) 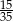 B)
B) 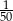 C)
C) 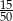 D)
D)