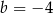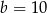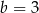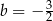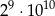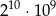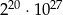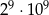W trakcie przygotowań do zawodów pływackich Szymon i Bartosz pływali równolegle do brzegu jeziora na dystansie 2 km. Wykresy przedstawiają zależność między odległością chłopców od miejsca startu, a czasem pływania.
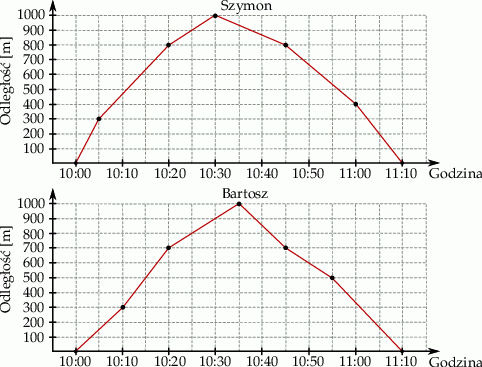
Ile razy między godziną 10:05 a 11:05 Szymon i Bartosz znajdowali się w tej samej odległości od miejsca startu?
A) 0 B) 1 C) 2 D) 4

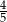

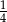
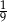
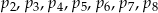 oznaczają prawdopodobieństwa, że na wylosowanej karteczce jest napisana liczba podzielna odpowiednio przez 2, 3, 4, 5, 6, 7, 8.
oznaczają prawdopodobieństwa, że na wylosowanej karteczce jest napisana liczba podzielna odpowiednio przez 2, 3, 4, 5, 6, 7, 8.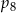 jest mniejsza od każdej z liczb:
jest mniejsza od każdej z liczb: 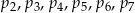 .
. 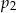 nie jest największą spośród liczb
nie jest największą spośród liczb 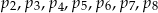 .
.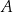 .
. 
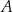 względem początku układu współrzędnych ma współrzędne
względem początku układu współrzędnych ma współrzędne 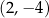
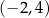
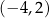
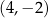
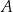 .
. 
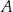 względem początku układu współrzędnych ma współrzędne
względem początku układu współrzędnych ma współrzędne 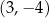
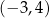
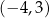
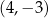
 , która spełnia nierówność
, która spełnia nierówność 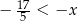
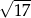 .
. 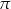 .
. 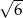 nie jest równa
nie jest równa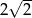
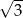
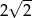
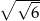
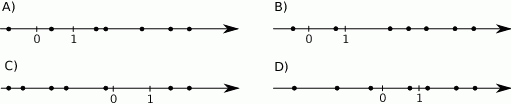


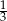

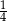 stanowiły piłeczki czarne. Wyciągnięto 12 piłeczek, wśród których żadna nie była czarna. Bartek – jako trzynasty – losuje jedną piłeczkę. Prawdopodobieństwo wylosowania przez Bartka piłeczki czarnej wynosi
stanowiły piłeczki czarne. Wyciągnięto 12 piłeczek, wśród których żadna nie była czarna. Bartek – jako trzynasty – losuje jedną piłeczkę. Prawdopodobieństwo wylosowania przez Bartka piłeczki czarnej wynosi 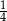
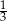
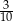
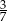
 stanowiły piłeczki czerwone. Wyciągnięto 16 piłeczek, wśród których żadna nie była czerwona. Kasia – jako siedemnasta – losuje jedną piłeczkę. Prawdopodobieństwo wylosowania przez Kasię piłeczki czerwonej wynosi
stanowiły piłeczki czerwone. Wyciągnięto 16 piłeczek, wśród których żadna nie była czerwona. Kasia – jako siedemnasta – losuje jedną piłeczkę. Prawdopodobieństwo wylosowania przez Kasię piłeczki czerwonej wynosi 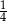
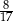
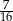
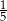
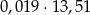 jest równa wartości wyrażenia
jest równa wartości wyrażenia 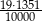 .
.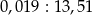 jest równa wartości wyrażenia
jest równa wartości wyrażenia 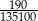 .
. 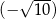 dodajemy 5. Otrzymany wynik jest liczbą
dodajemy 5. Otrzymany wynik jest liczbą 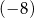 .
. 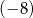 .
. 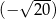 dodajemy 5. Otrzymany wynik jest liczbą
dodajemy 5. Otrzymany wynik jest liczbą 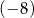 .
. 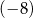 .
.  . Ile kulek zielonych usunięto z pudełka?
. Ile kulek zielonych usunięto z pudełka?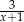 i przeciwnej do
i przeciwnej do 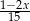 jest równa
jest równa 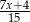
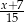
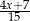
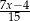
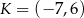 i
i 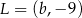 są końcami odcinka
są końcami odcinka 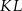 . Pierwsza współrzędna środka odcinka
. Pierwsza współrzędna środka odcinka 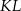 jest o 3 większa od jego drugiej współrzędnej. Wynika stąd, że
jest o 3 większa od jego drugiej współrzędnej. Wynika stąd, że