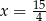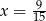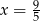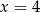Z kartonu wykonano modele sześcianu i graniastosłupa prawidłowego czworokątnego. Podstawa sześcianu jest taka sama jak podstawa graniastosłupa. Na wykonanie sześcianu zużyto 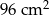 kartonu, a na graniastosłup o
kartonu, a na graniastosłup o 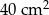 więcej (nie wliczając powierzchni zakładek).
więcej (nie wliczając powierzchni zakładek).
Korzystając z powyższych informacji, oceń prawdziwość poniższych zdań (P – prawda, F – fałsz).
Na wykonanie jednej ściany sześcianu zużyto 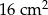 kartonu. kartonu. | P | F |
| Podstawą każdej z tych brył jest kwadrat o boku 4 cm. | P | F |
Pole powierzchni bocznej graniastosłupa jest równe 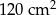 . . | P | F |
| Wysokość graniastosłupa jest równa 6 cm. | P | F |

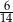
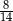

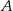 i
i 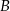 są odpowiednio równe 2018 i 995. Długość odcinka
są odpowiednio równe 2018 i 995. Długość odcinka 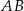 jest równa 1020.
jest równa 1020. 
 jest mniejsza od 1023.
jest mniejsza od 1023.  jest mniejsza od promienia większego okręgu.
jest mniejsza od promienia większego okręgu. 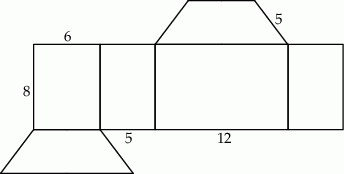
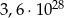 i
i 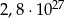 jest równa:
jest równa: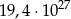
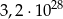
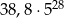
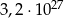
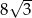
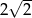
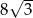
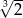
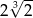
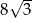
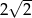
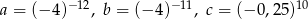 .
. 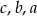
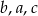
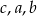
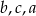
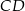 trójkąta
trójkąta 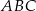 ma długość 12, bok
ma długość 12, bok 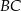 ma długość 37, a odcinek
ma długość 37, a odcinek 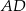 ma długość 5 (zobacz rysunek).
ma długość 5 (zobacz rysunek). 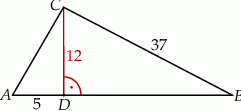
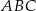 jest równe A/B.
jest równe A/B.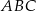 jest równy C/D.
jest równy C/D.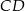 trójkąta
trójkąta 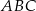 ma długość 12, bok
ma długość 12, bok  ma długość 37, a odcinek
ma długość 37, a odcinek  ma długość 5 (zobacz rysunek).
ma długość 5 (zobacz rysunek). 
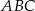 jest prostokątny.
jest prostokątny. 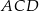 jest równa
jest równa 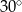 .
.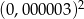 jest równa
jest równa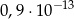
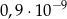
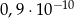
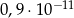
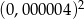 jest równa
jest równa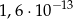
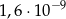
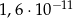
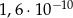
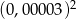 jest równa
jest równa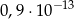
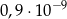
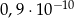
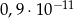

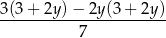
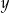 :
: 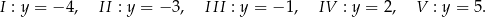
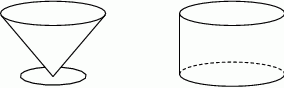
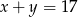 i
i 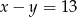 to
to 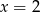
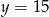
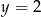
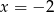
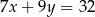 i
i 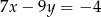 to
to 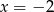
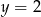
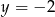
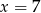
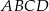 o podstawach długości 22 cm, 10 cm i wysokości 5 cm. Odcinek
o podstawach długości 22 cm, 10 cm i wysokości 5 cm. Odcinek 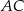 jest przekątną tego trapezu.
jest przekątną tego trapezu. 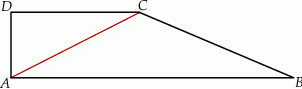
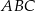 jest równoramienny.
jest równoramienny.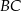 ma długość 12 cm.
ma długość 12 cm. 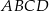 o podstawach długości 10 cm, 6 cm i ramieniu długości
o podstawach długości 10 cm, 6 cm i ramieniu długości 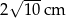 . Odcinek
. Odcinek 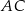 jest przekątną tego trapezu.
jest przekątną tego trapezu. 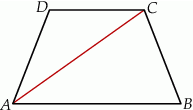
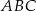 jest równoramienny.
jest równoramienny. 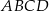 , w którym trójkąt
, w którym trójkąt  jest trójkątem równobocznym o boku długości 6 cm.
jest trójkątem równobocznym o boku długości 6 cm. 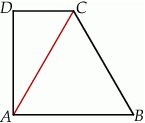
 powiększymy o 3, to otrzymamy
powiększymy o 3, to otrzymamy  tej liczby. Wynika stąd, że
tej liczby. Wynika stąd, że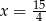
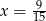
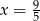
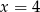
 powiększymy o 4, to otrzymamy
powiększymy o 4, to otrzymamy 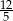 tej liczby. Wynika stąd, że
tej liczby. Wynika stąd, że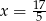
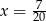
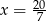
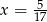
 powiększymy o 5, to otrzymamy
powiększymy o 5, to otrzymamy  tej liczby. Wynika stąd, że
tej liczby. Wynika stąd, że