W trapezie równoramiennym o obwodzie 21 cm suma długości ramienia i krótszej podstawy jest równa 8 cm. Różnica długości podstaw tego trapezu jest równa
A) 10 cm B) 13 cm C) 5 cm D) 2,5 cm
/Szkoła podstawowa/Zadania testowe
Na rysunku przedstawiono okrąg wpisany w trójkąt.
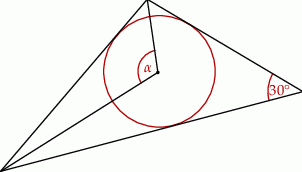
Miara kąta  jest równa
jest równa
A) 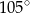 B)
B) 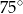 C)
C) 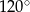 D)
D) 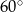
Okrąg o środku w punkcie 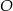 jest wpisany w trójkąt
jest wpisany w trójkąt 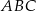 . Wiadomo, że
. Wiadomo, że 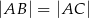 i
i 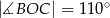 (zobacz rysunek).
(zobacz rysunek).
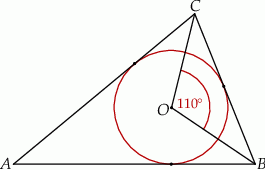
Miara kąta 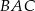 jest równa
jest równa
A) 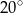 B)
B) 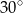 C)
C) 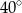 D)
D) 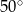
Okrąg o środku w punkcie 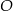 jest wpisany w trójkąt
jest wpisany w trójkąt 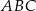 . Wiadomo, że
. Wiadomo, że 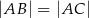 i
i 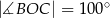 (zobacz rysunek).
(zobacz rysunek).
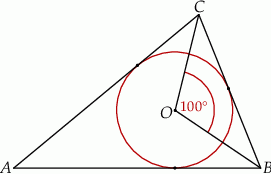
Miara kąta 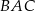 jest równa
jest równa
A) 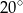 B)
B) 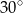 C)
C) 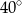 D)
D) 
Kwadrat o boku  przedstawiony na rysunku I rozcięto na dwa przystające prostokąty, z których ułożono figurę, jak na rysunku II – jeden z prostokątów nałożono na drugi prostokąt.
przedstawiony na rysunku I rozcięto na dwa przystające prostokąty, z których ułożono figurę, jak na rysunku II – jeden z prostokątów nałożono na drugi prostokąt.
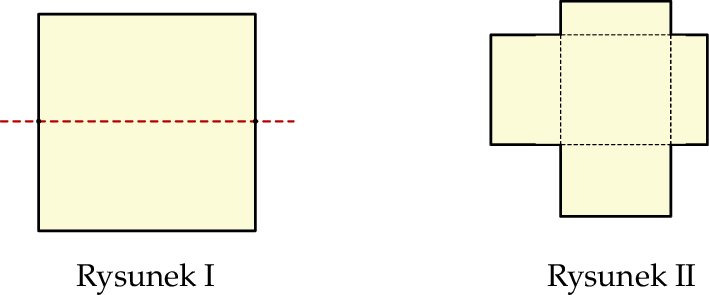
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Obwód ułożonej figury jest dwa razy większy od obwodu kwadratu. | P | F |
Pole ułożonej figury jest równe 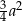 . . | P | F |
Punkt 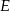 jest środkiem boku
jest środkiem boku 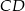 kwadratu
kwadratu 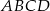 .
.
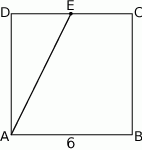
Długość odcinka 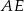 jest równa
jest równa
A) 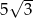 B)
B) 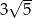 C)
C) 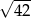 D)
D) 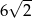
Które zdanie jest fałszywe?
A) Suma kolejnych trzech liczb naturalnych jest liczbą podzielną przez 3.
B) Iloczyn kolejnych trzech liczb naturalnych jest liczbą podzielną przez 3.
C) Suma trzech kolejnych liczb parzystych jest liczbą podzielną przez 3.
D) Iloczyn trzech różnych nieparzystych liczb naturalnych jest liczbą podzielną przez 3.
Na którym rysunku zamalowano 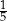 figury?
figury?

Pan Jerzy wyjechał samochodem z miasta 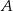 do miasta
do miasta 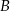 o godzinie 9:30. Odległość miasta
o godzinie 9:30. Odległość miasta 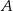 od miasta
od miasta  jest równa 210 km. Wykres przedstawia zależność drogi przebytej przez pana Jerzego od czasu jazdy.
jest równa 210 km. Wykres przedstawia zależność drogi przebytej przez pana Jerzego od czasu jazdy.
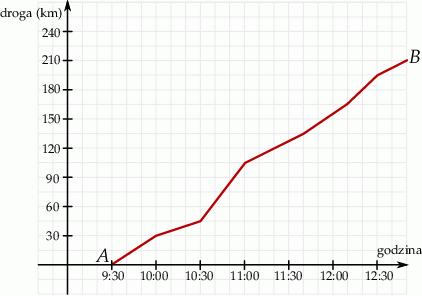
Zaznacz P, jeśli zdanie jest prawdziwe, lub zaznacz F – jeśli jest fałszywe.
| Do godziny 10:30 pan Jerzy przejechał 45 km. | P | F |
Do miasta  pan Jerzy przyjechał o godzinie 13:00. pan Jerzy przyjechał o godzinie 13:00. | P | F |
Pan Jerzy wyjechał z pewnego miasta samochodem w trasę liczącą 210 km o godzinie 9:30. Dziesięć minut później z tego samego miasta wyjechał w tę samą trasę pan Wojciech. Wykresy przedstawiają zależność drogi przebytej przez obu kierowców od czasu jazdy.
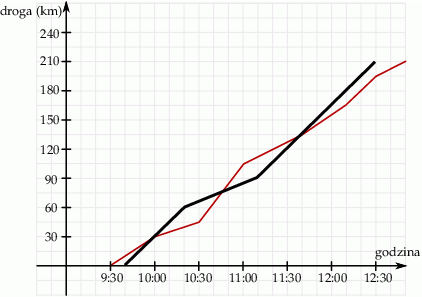
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| O godzinie 10:30 bliżej celu był pan Wojciech. | P | F |
| Większą średnią prędkość na całej trasie uzyskał samochód pana Jerzego. | P | F |
Szklane naczynie, którego podstawa ma kształt prostopadłościanu o wymiarach 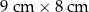 zostało wypełnione wodą do wysokości 12 cm. Następnie woda ta została przelana do drugiego szklanego naczynia, którego podstawa ma wymiary
zostało wypełnione wodą do wysokości 12 cm. Następnie woda ta została przelana do drugiego szklanego naczynia, którego podstawa ma wymiary 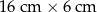 .
.
Do jakiej wysokości sięga woda w drugim naczyniu?
A) 9 cm B) 11 cm C) 10 cm D) 12 cm
Doświadczenie losowe polega na dwukrotnym rzucie monetą. Jeśli wypadnie orzeł, zapisujemy 1, a jeśli reszka – zapisujemy 2. Wynikiem doświadczenia jest zapisana liczba dwucyfrowa. Jakie jest prawdopodobieństwo, że zapisana liczba jest podzielna przez 3?
A) 0 B) 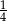 C)
C) 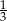 D)
D) 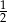
Doświadczenie losowe polega na dwukrotnym rzucie monetą. Jeśli wypadnie orzeł, zapisujemy 6, a jeśli reszka – zapisujemy 4. Wynikiem doświadczenia jest zapisana liczba dwucyfrowa. Jakie jest prawdopodobieństwo, że zapisana liczba jest podzielna przez 3?
A) 0 B) 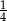 C)
C) 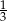 D)
D) 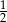
W grudniu, w trzech sklepach sportowych: Alfa, Beta i Gamma, sprzedawano łyżwy figurowe w tej samej cenie. Na wiosnę w każdym sklepie ogłoszono obniżkę cen tych łyżew. Poniżej przedstawiono oferty tych sklepów.

Po obniżce cena łyżew figurowych była
A) najniższa w sklepie Alfa. B) najniższa w sklepie Beta.
C) najniższa w sklepie Gamma. D) taka sama w trzech sklepach.
W październiku, w trzech hurtowniach budowlanych: Alfa, Beta i Gamma, sprzedawano styropian w tej samej cenie. Na wiosnę, w wyniku wzrostu kosztów produkcji styropianu, w każdym ze sklepów wywieszono informację o podwyżce. Poniżej przedstawiono oferty tych hurtowni.

Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Po podwyżce najniższa cena styropianu była w hurtowni Alfa. | P | F |
| Po podwyżce w jednej z hurtowni cena styropianu wzrosła o ponad 30 | P | F |
W układzie współrzędnych zaznaczono dwa wierzchołki kwadratu 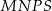 , które nie należą do tego samego boku.
, które nie należą do tego samego boku.
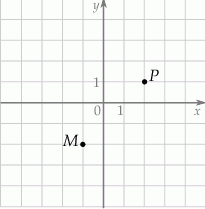
Dwa pozostałe wierzchołki tego kwadratu mają współrzędne
A) 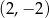 i
i 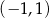 B)
B) 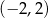 i
i 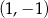 C)
C) 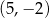 i
i 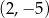 D)
D) 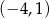 i
i 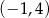
W układzie współrzędnych zaznaczono dwa wierzchołki kwadratu 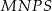 , które nie należą do tego samego boku.
, które nie należą do tego samego boku.
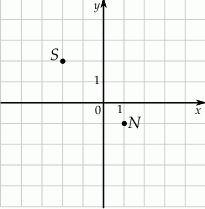
Dwa pozostałe wierzchołki tego kwadratu mają współrzędne
A) 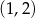 i
i 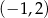 B)
B) 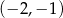 i
i 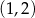 C)
C) 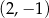 i
i 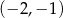 D)
D) 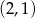 i
i 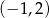
Punkty 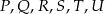 są środkami boków sześciokąta foremnego
są środkami boków sześciokąta foremnego 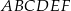 (rysunek).
(rysunek).
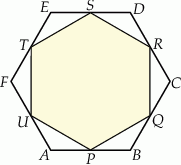
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole trójkąta 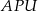 stanowi stanowi 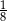 pola sześciokąta pola sześciokąta 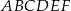 . . | P | F |
Pole sześciokąta 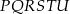 stanowi stanowi  pola sześciokąta pola sześciokąta 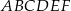 . . | P | F |
W sześciokącie foremnym 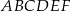 poprowadzono trzy przekątne i otrzymano trójkąt
poprowadzono trzy przekątne i otrzymano trójkąt 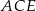 .
.
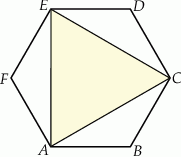
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Obwód trójkąta 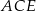 jest większy niż jest większy niż 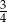 obwodu sześciokąta obwodu sześciokąta 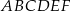 . . | P | F |
Pole trójkąta 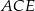 stanowi połowę pola sześciokąta stanowi połowę pola sześciokąta 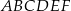 . . | P | F |
W trójkącie prostokątnym 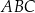 przyprostokątną
przyprostokątną 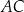 wydłużono o 7 cm, a przyprostokątną
wydłużono o 7 cm, a przyprostokątną 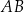 wydłużono o 12 cm i otrzymano trójkąt prostokątny równoramienny
wydłużono o 12 cm i otrzymano trójkąt prostokątny równoramienny 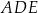 o polu równym
o polu równym 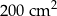 .
.
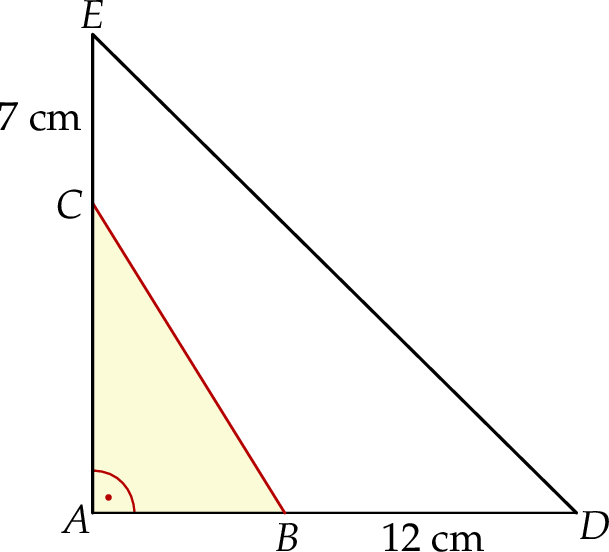
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Przyprostokątna trójkąta 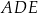 jest równa 20 cm. jest równa 20 cm. | P | F |
Pole trójkąta 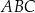 jest równe jest równe 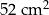 . . | P | F |
Pierwsza rata, która stanowi 9% ceny kanapy, jest o 84 zł niższa od drugiej raty, która stanowi 12% ceny kanapy. Kanapa kosztuje
A) 280 zł B) 2788 zł C) 2520 zł D) 2800 zł
Pierwsza rata, która stanowi 10% ceny aparatu, jest o 19 zł niższa od drugiej raty, która stanowi 15% ceny aparatu. Aparat kosztuje
A) 380 zł B) 38 zł C) 420 zł D) 360 zł
W klasie jest cztery razy więcej chłopców niż dziewcząt. Ile procent wszystkich uczniów tej klasy stanowią dziewczęta?
A) 4% B) 5% C) 20% D) 25%
W loterii fantowej jest 9 razy więcej losów przegrywających niż wygrywających. Ile procent wszystkich losów w tej loterii stanowią losy wygrywające?
A) 1% B) 11% C) 10% D) 90%
Ze zbioru liczb 3, 4, 1, 5, 1, 3, 1 usunięto jedną liczbę w ten sposób, że mediana tego zbioru liczb nie uległa zmianie. Usunięta liczba to
A) 1 B) 3 C) 4 D) 5
Na diagramie kołowym przedstawiono procentowy udział soków o różnych smakach, które zostały sprzedane podczas festynu. Najmniej sprzedano soku pomidorowego, tylko 15 kartonów, a najwięcej – soku jabłkowego.
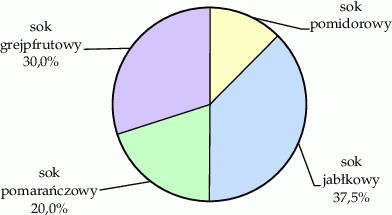
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Sprzedano łącznie 125 kartonów soków. | P | F |
| Sprzedano o 30 kartonów więcej soku jabłkowego niż pomidorowego. | P | F |
Punkty 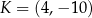 i
i 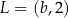 są końcami odcinka
są końcami odcinka 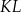 . Pierwsza współrzędna środka odcinka
. Pierwsza współrzędna środka odcinka 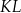 jest równa
jest równa 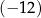 . Wynika stąd, że
. Wynika stąd, że
A) 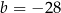 B)
B) 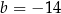 C)
C) 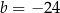 D)
D) 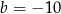
W układzie współrzędnych narysowano sześciokąt foremny o boku 2 tak, że jednym z jego wierzchołków jest punkt 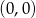 , a jeden z jego boków leży na osi
, a jeden z jego boków leży na osi  (rysunek).
(rysunek).
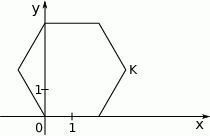
Współrzędne wierzchołka K tego sześciokąta są równe
A) 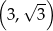 B)
B) 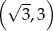 C)
C) 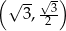 D)
D) 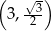
W układzie współrzędnych narysowano kwadrat o przekątnej długości 4 tak, że jednym z jego wierzchołków jest punkt 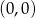 , a jedna z jego przekątnych jest równoległa do osi
, a jedna z jego przekątnych jest równoległa do osi 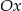 .
.
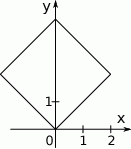
Długość boku kwadratu jest równa
A) 2 B) 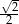 C)
C) 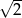 D)
D) 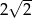
W układzie współrzędnych narysowano trójkąt równoboczny tak, że jednym z jego wierzchołków jest punkt 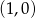 , jeden z wierzchołków jest na osi
, jeden z wierzchołków jest na osi 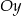 , a jeden z jego boków jest równoległy do osi
, a jeden z jego boków jest równoległy do osi 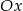 (zobacz rysunek).
(zobacz rysunek).
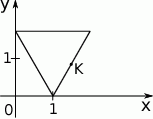
Współrzędne środka 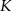 boku trójkąta są równe
boku trójkąta są równe
A) 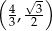 B)
B) 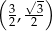 C)
C) 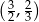 D)
D) 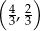
Na rysunku przedstawiono sposób w jaki ustawia się krzesła w pewnej restauracji w zależności od liczby połączonych stołów.
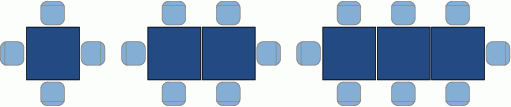
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W układzie z 14 połączonymi stołami jest 30 krzeseł. | P | F |
| Jeżeli podwajamy liczbę stołów w układzie, to liczba krzeseł też rośnie dwukrotnie. | P | F |

