Zadanie nr 5531079
Dany jest trapez równoramienny 
o podstawach długości 10 cm, 6 cm i ramieniu długości 
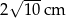. Odcinek 
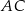jest przekątną tego trapezu.
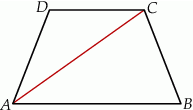
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąt 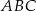 jest równoramienny. | P | F |
| Wysokość trapezu ma długość 5 cm. | P | F |
Rozwiązanie
Dorysujmy wysokości trapezu.
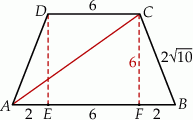
Mamy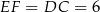 
i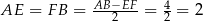 
.
Stosując twierdzenie Pitagorasa w trójkącie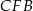 
obliczamy długość wysokości trapezu.
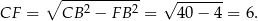
Teraz z trójkąta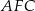 
obliczamy długość przekątnej trapezu.
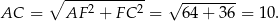
Zatem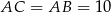 
i rzeczywiście trójkąt 
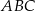jest równoramienny.
Odpowiedź: P, F
