/Szkoła podstawowa/Zadania testowe

Zadanie nr 9890500

Dodaj do ulubionych
Dodaj do rozwiązanych

Równoległobok, w którym stosunek długości sąsiednich boków wynosi 2:3, podzielono wzdłuż przekątnej o długości 13 cm na dwa przystające trójkąty. Obwód każdego z tych trójkątów jest równy 33 cm. Czy podane zdania są prawdziwe?

Równoległobok ma obwód 40 cm. PF
Równoległobok ma bok o długości 12 cm. PF
Jeden z boków równoległoboku jest dwa razy krótszy od drugiego.PF

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

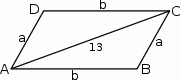
Przy oznaczeniach z rysunku mamy układ równań

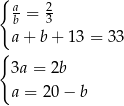
{ ab = 23 a + b + 13 = 33 { 3a = 2b a = 20 − b

Podstawmy 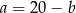a = 20− b do pierwszego równania

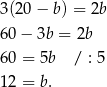
3(20− b) = 2b 60− 3b = 2b 60 = 5b / : 5 12 = b.

Stąd 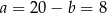a = 20 − b = 8 . Obwód równoległoboku wynosi

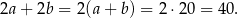
2a+ 2b = 2(a + b) = 2 ⋅20 = 40.

 
Odpowiedź: P, P, F

Wersja PDF