Zadanie nr 4829897
Jabłka i gruszki pakowano do pojemników, przy czym do jednego pojemnika wkładano 64 gruszki lub 80 jabłek. Po zapakowaniu owoców okazało się, że zapakowano dokładnie tyle samo jabłek, co gruszek.
Jaka jest najmniejsza możliwa liczba pojemników, do których zapakowano te owoce?
A) 5 B) 18 C) 9 D) 4
Rozwiązanie
Jeżeli oznaczymy przez  liczbę zapakowanych jabłek, to
liczbę zapakowanych jabłek, to  jest też liczbą zapakowanych gruszek. Liczba
jest też liczbą zapakowanych gruszek. Liczba  musi się dzielić przez 64 i przez 80, więc jej najmniejsza możliwa wartość to najmniejsza wspólna wielokrotność 64 i 80. Zauważmy, że
musi się dzielić przez 64 i przez 80, więc jej najmniejsza możliwa wartość to najmniejsza wspólna wielokrotność 64 i 80. Zauważmy, że
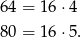
Zatem najmniejsza możliwa wartość  to
to
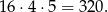
Do zapakowania jabłek użyto więc 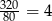 pojemników, a do zapakowania gruszek
pojemników, a do zapakowania gruszek 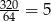 pojemników. W sumie użyto więc
pojemników. W sumie użyto więc 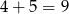 pojemników.
pojemników.
Odpowiedź: C

