Średnie zużycie paliwa na pierwszym odcinku trasy było równe 7 litrów na 100 kilometrów, a średnie zużycie paliwa na drugim, dwa razy dłuższym odcinku trasy, było równe 10 litrów na 100 kilometrów. Średnie zużycie paliwa na każde 100 km całej trasy wyniosło
A) 8 litrów. B) 8,5 litra. C) 7 litrów. D) 9 litrów.
/Szkoła podstawowa/Zadania testowe/Zadania z treścią/Prędkość, droga, czas
Samolot pasażerski spala średnio 10 ton paliwa w ciągu godziny lotu.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W ciągu minuty lotu samolot spala ponad 200 kg paliwa. | P | F |
| Spalenie przez samolot 1800 kg paliwa trwa krócej niż 12 minut. | P | F |
Zosia czyta  stron książki w ciągu
stron książki w ciągu 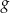 godzin. Wynika stąd, że w ciągu
godzin. Wynika stąd, że w ciągu 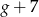 godzin przeczyta stron
godzin przeczyta stron
A) 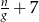 B)
B) 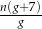 C)
C) 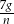 D)
D) 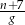
Kasia czyta  stron książki w ciągu
stron książki w ciągu 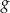 godzin. Wynika stąd, że w ciągu
godzin. Wynika stąd, że w ciągu 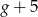 godzin przeczyta stron
godzin przeczyta stron
A) 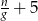 B)
B) 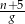 C)
C) 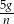 D)
D) 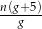
Jacek czyta średnio 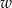 wyrazów w ciągu
wyrazów w ciągu 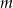 minut. Wynika stąd, że w ciągu
minut. Wynika stąd, że w ciągu 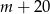 minut przeczyta wyrazów
minut przeczyta wyrazów
A) 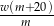 B)
B) 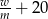 C)
C) 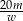 D)
D) 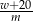
Grupa turystów w ciągu pierwszej godziny marszu pokonała pewien odcinek trasy. W każdej następnej godzinie pokonywany dystans był o 0,5 km krótszy od dystansu pokonanego w poprzedniej godzinie. W ciągu pierwszych pięciu godzin marszu turyści przeszli łącznie 17,5 km trasy. Odcinek trasy, który turyści przeszli w pierwszej godzinie marszu, miał długość
A) 3,1 km B) 3,5 km C) 3,9 km D) 4,0 km E) 4,5 km
Grupa turystów w ciągu pierwszej godziny marszu pokonała pewien odcinek trasy. W każdej następnej godzinie pokonywany dystans był o 0,5 km dłuższy od dystansu pokonanego w poprzedniej godzinie. W ciągu pierwszych sześciu godzin marszu turyści przeszli łącznie 16,5 km trasy. Odcinek trasy, który turyści przeszli w pierwszej godzinie marszu, miał długość
A) 4 km B) 2,5 km C) 3,5 km D) 1,5 km E) 2,1 km
Kasia zauważyła, że ścienny zegar w mieszkaniu babci w ciągu każdej godziny spóźnia się o kolejne 4 minuty. Gdy poprawnie działający zegarek Kasi wskazywał godzinę 9:00, dziewczynka ustawiła na zegarze ściennym tę samą godzinę. Przyjęła, że w każdym kolejnym kwadransie opóźnienie jest jednakowe. Którą godzinę wskaże – zgodnie z założeniami Kasi – zegar ścienny po upływie 2 godzin i 3 kwadransów od godziny 9:00, jeżeli zachowana zostanie zaobserwowana tendencja opóźniania?
A) 11:34 B) 11:37 C) 11:41 D) 11:56
Uczestnicy obozu wędrownego w ciągu drugiego dnia marszu pokonali dwa razy dłuższy odcinek trasy niż w ciągu pierwszego dnia, a w ciągu trzeciego dnia marszu pokonali dystans trzy razy krótszy niż drugiego dnia. W sumie w ciągu trzech dni pokonali trasę długości 60,5 km. Odcinek trasy, który turyści przeszli w drugim dniu wędrówki miał długość
A) 16,5 km B) 33 km C) 36 km D) 11 km
Samochód połowę drogi przebył ze średnią prędkością 30 km/h, a drugą połowę drogi ze średnią prędkością 60 km/h. Zatem średnia prędkość samochodu na całej trasie jest równa
A) 40 km/h B) 45 km/h C) 50 km/h D) 55 km/h
Rowerzysta połowę górskiej trasy pokonał ze średnią prędkością 8 km/h, a drugą połowę tej trasy pokonał ze średnią prędkością 24 km/h. Zatem średnia prędkość rowerzysty na całej trasie jest równa
A) 10 km/h B) 12 km/h C) 16 km/h D) 18 km/h
Tata Bartka przed wyjazdem z Krakowa do Warszawy analizuje niektóre bezpośrednie połączenia między tymi miastami. Do wyboru ma cztery połączenia przedstawione w poniższej tabeli.
| Godzina wyjazdu z Krakowa | Godzina przyjazdu do Warszawy | Środek transportu | Długość trasy | Cena biletu |
| 1:35 | 6:30 | autobus | 298 km | 27 zł |
| 2:32 | 5:12 | pociąg | 293 km | 60 zł |
| 5:00 | 8:48 | pociąg | 364 km | 65 zł |
| 5:53 | 8:10 | pociąg | 293 km | 49 zł |
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Za przejazd w najkrótszym czasie należy zapłacić 49 zł. | P | F |
| Zgodnie z rozkładem jazdy tylko przejazd autobusem trwa dłużej niż 4 godziny. | P | F |
Tata Kamila przed wyjazdem z Warszawy do Krakowa analizuje niektóre bezpośrednie połączenia między tymi miastami. Do wyboru ma cztery połączenia przedstawione w poniższej tabeli.
| Godzina wyjazdu z Warszawy | Godzina przyjazdu do Krakowa | Środek transportu | Długość trasy | Cena biletu |
| 1:35 | 6:30 | autobus | 298 km | 27 zł |
| 2:32 | 5:12 | pociąg | 293 km | 60 zł |
| 4:36 | 8:48 | pociąg | 364 km | 58 zł |
| 5:53 | 8:10 | pociąg | 293 km | 65 zł |
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Za przejazd w najkrótszym czasie należy zapłacić 65 zł. | P | F |
| Zgodnie z rozkładem jazdy tylko przejazd autobusem trwa dłużej niż 4 godziny. | P | F |
Hania pokonuje drogę 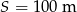 z domu do szkoły w czasie 30 min. Z jaką średnią prędkością idzie Hania?
z domu do szkoły w czasie 30 min. Z jaką średnią prędkością idzie Hania?
A) 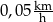 B)
B) 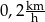 C)
C) 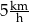 D)
D) 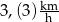
Paweł przejechał na rowerze trasę długości 700 m w czasie 2 min. Prędkość średnia, jaką uzyskał Paweł na tej trasie, jest równa
A) 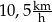 B)
B) 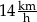 C)
C) 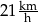 D)
D) 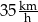
Samochód przejechał ze stałą prędkością trasę o długości 18 kilometrów w czasie 12 minut. Samochód przejechał tę trasę z prędkością
A) 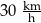 B)
B) 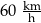 C)
C) 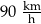 D)
D) 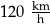
Kasia przejechała na rowerze trasę długości 900 m w czasie 3 min. Prędkość średnia, jaką uzyskała Kasia na tej trasie, jest równa
A) 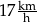 B)
B) 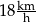 C)
C) 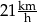 D)
D) 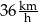
Sonda Voyager 2, która została wysłana w przestrzeń kosmiczną w 1977 roku, w 2007 roku znalazła się na granicy heliosfery w odległości 17,5 bilionów kilometrów od słońca. Od tej pory sonda oddala się od słońca ze stałą prędkością równą 15,35 km/s. Prędkość sondy Voyager 2 po opuszczeniu heliosfery jest równa
A) 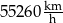 B)
B) 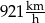 C)
C) 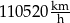 D)
D) 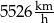
W pewnym zakładzie każdy z pracowników codziennie maluje taką samą liczbę jednakowych ozdób. Pracownicy potrzebowali 12 dni roboczych, aby wykonać zamówienie. Gdyby było ich o dwóch więcej, to czas wykonania tego zamówienia byłby o 3 dni krótszy. Liczbę pracowników  tego zakładu można obliczyć, rozwiązując równanie
tego zakładu można obliczyć, rozwiązując równanie
A) 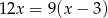 B)
B) 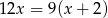 C)
C) 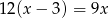 D)
D) 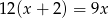
Maszyna produkcyjna wytwarza codziennie tę samą liczbę elementów. Wykonanie pewnego zamówienia wymaga jednoczesnej pracy pewnej liczby takich maszyn przez 15 dni. Gdyby jednak zwiększyć liczbę pracujących maszyn o 4, to czas wykonania zamówienia skróciłby się o 2 dni. Liczbę maszyn potrzebnych do realizacji zamówienia można obliczyć, rozwiązując równanie
A) 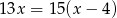 B)
B) 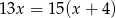 C)
C) 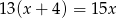 D)
D) 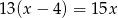
Robotnicy pracowali trzy dni przy układaniu chodnika. Pierwszego dnia robotnicy ułożyli 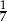 chodnika, drugiego dnia ułożyli
chodnika, drugiego dnia ułożyli 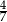 chodnika, a trzeciego resztę. Jaką część chodnika robotnicy ułożyli trzeciego dnia?
chodnika, a trzeciego resztę. Jaką część chodnika robotnicy ułożyli trzeciego dnia?
A) 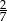 B)
B) 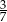 C)
C) 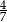 D)
D) 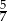
Miejscowości 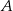 i
i 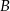 położone na przeciwległych brzegach jeziora są połączone dwiema drogami – drogą polną prowadzącą przez punkt
położone na przeciwległych brzegach jeziora są połączone dwiema drogami – drogą polną prowadzącą przez punkt 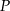 i drogą leśną prowadzącą przez punkt
i drogą leśną prowadzącą przez punkt 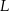 . Długość drogi polnej
. Długość drogi polnej 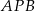 wynosi 10 km, a długość drogi leśnej
wynosi 10 km, a długość drogi leśnej 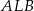 jest równa 6 km.
jest równa 6 km.
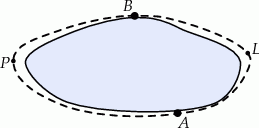
Matylda i Karol wyruszyli na rowerach z miejscowości 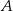 do miejscowości
do miejscowości 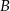 o godzinie 10:00. Matylda jechała drogą leśną, a Karol – drogą polną. Średnia prędkość jazdy Matyldy wynosiła
o godzinie 10:00. Matylda jechała drogą leśną, a Karol – drogą polną. Średnia prędkość jazdy Matyldy wynosiła 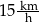 , a średnia prędkość Karola była równa
, a średnia prędkość Karola była równa 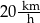 .
.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Do miejscowości 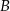 Karol przyjechał wcześniej niż Matylda. Karol przyjechał wcześniej niż Matylda. | P | F |
Matylda przyjechała do miejscowości 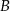 o godzinie 10:24. o godzinie 10:24. | P | F |
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
15 minut to 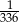 tygodnia. tygodnia. | P | F |
12 sekund to 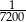 doby. doby. | P | F |
Piłkę tenisową puszczono swobodnie z pewnej wysokości. Wzór 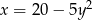 opisuje zależność wysokości
opisuje zależność wysokości  (w metrach) na jakiej znajduje się piłka od czasu
(w metrach) na jakiej znajduje się piłka od czasu 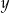 (w sekundach), który upłynął od momentu puszczenia piłki. Który wykres przedstawia tę zależność?
(w sekundach), który upłynął od momentu puszczenia piłki. Który wykres przedstawia tę zależność?
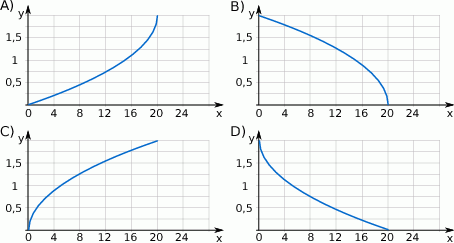
Dwunastu malarzy pracując z jednakową wydajnością pomalowało burtę statku w ciągu 8 godzin. Ilu malarzy powinno malować tę burtę, aby tę samą pracę wykonać w ciągu 6 godzin?
A) 14 B) 16 C) 18 D) 20
Osiem pomp napełnia cały zbiornik w ciągu 6 godzin. Każda pompa pracuje z taką samą stałą wydajnością. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Sześć pomp napełni cały zbiornik w ciągu 9 godzin. | P | F |
| Połowę zbiornika w ciągu 4 godzin napełni 6 pomp. | P | F |
Sześć maszyn produkuje pewną partię jednakowych butelek z tworzywa sztucznego przez 4 godziny. Każda z maszyn pracuje z taką samą stałą wydajnością.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Przez 8 godzin taką samą partię butelek wykonają 3 takie maszyny. | P | F |
| Połowę partii takich butelek 6 maszyn wykona przez 2 godziny. | P | F |
W pewnej fabryce są dwie linie produkcyjne produkujące identyczne układy elektroniczne. Obydwie linie produkcyjne wytwarzają łącznie 720 układów w ciągu 8 godzin, a sama druga linia produkcyjna wytwarza 558 układów w ciągu 12 godzin.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Pierwsza linia produkcyjna pracuje z mniejszą wydajnością niż druga. | P | F |
| Pierwsza linia produkcyjna w ciągu 8 godzin wykonuje 352 układy. | P | F |
W pewnym zakładzie pracy każdy z pracowników codziennie montuje taką samą liczbę jednakowych podzespołów. Pracownicy potrzebowali 12 dni roboczych, aby wykonać zamówienie. Gdyby wydajność każdego z pracowników była wyższa o 20%, to wykonaliby zamówienie w
A) 8 dni B) 9 dni C) 10 dni D) 11 dni
W ciągu dwóch godzin trzy jednakowe maszyny produkują razem 1200 guzików. Ile guzików wyprodukuje pięć takich maszyn w ciągu jednej godziny? Przyjmij, że maszyny pracują z taką samą, stałą wydajnością.
A) 800 B) 900 C) 1000 D) 1500
W ciągu trzech godzin dwie jednakowe maszyny produkują razem 1200 guzików. Ile guzików wyprodukuje pięć takich maszyn w ciągu dwóch godzin? Przyjmij, że maszyny pracują z taką samą, stałą wydajnością.
A) 2000 B) 900 C) 1000 D) 1500
Rowerzysta uczestniczył w rajdzie rowerowym. Całą trasę rajdu pokonał w ciągu czterech dni. W tabeli poniżej przedstawiono długości kolejnych etapów trasy, które przebył każdego dnia.
| Dzień | Długość kolejnych etapów trasy (w km) |
| poniedziałek | 26 |
| wtorek | 27 |
| środa | 21 |
| czwartek | 31 |
W poniedziałek i wtorek rowerzysta przejechał łącznie A/B długości całej trasy rajdu .
A) więcej niż 50% B) mniej niż 50%
W środę rowerzysta przejechał C/D długości całej trasy rajdu.
C) 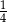 D)
D) 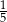
Tomek uczestniczył w czterodniowej wycieczce pieszej. W tabeli poniżej przedstawiono długości kolejnych etapów trasy, które przebył każdego dnia.
| Dzień | Długość kolejnych etapów trasy (w km) |
| wtorek | 24 |
| środa | 13 |
| czwartek | 15 |
| piątek | 20 |
W czwartek i piątek Tomek pokonał łącznie A/B długości całej trasy wycieczki.
A) więcej niż 50% B) mniej niż 50%
We wtorek Tomek przebył C/D długości całej trasy rajdu.
C) 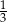 D)
D) 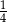
Dwa pojazdy poruszają w tym samym kierunku wokół okrągłego toru o długości 1,8 km. Pojazdy startują w tym samym czasie i pierwszy z nich porusza się z prędkością 15 m/s, a drugi porusza się z prędkością 12 m/s. Pojazdy ponownie spotkają się w miejscu startu po
A) 20 minutach B) 10 minutach C) 1 godzinie D) 30 minutach
Prędkość rozchodzenia się impulsu elektrycznego u człowieka wynosi około 2 metrów na sekundę. U roślin impuls elektryczny może rozchodzić się z prędkością około 60 centymetrów na minutę. Ile razy prędkość rozchodzenia się impulsu elektrycznego u człowieka jest większa od prędkości rozchodzenia się impulsu elektrycznego u roślin?
A) W przybliżeniu 2 razy. B) W przybliżeniu 20 razy.
C) W przybliżeniu 200 razy. D) W przybliżeniu 2000 razy.

