/Szkoła podstawowa/Zadania testowe/Geometria/Prostokąt

Zadanie nr 8987681

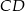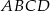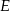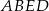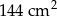Na boku CD prostokąta ABCD o bokach długości 12 cm i 20 cm wybrano punkt E w ten sposób, że pole czworokąta ABED jest równe 144 cm 2 .

PIC

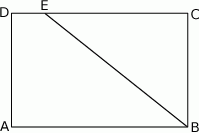
Długość odcinka 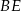BE jest równa
A) 20 B) 24 C) 18 D) 16

Wersja PDF

Rozwiązanie

Pole całego prostokąta jest równe 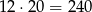1 2⋅20 = 240 , więc pole trójkąta 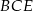BCE jest równe

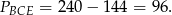
PBCE = 240 − 14 4 = 96.

Z drugiej strony,

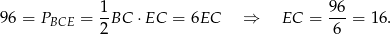
96 = PBCE = 1BC ⋅EC = 6EC ⇒ EC = 96-= 16. 2 6

Teraz korzystamy z twierdzenia Pitagorasa.

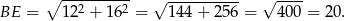
∘ ---------- √ ---------- √ ---- BE = 122 + 162 = 14 4+ 256 = 400 = 20.

 
Odpowiedź: A

Wersja PDF