/Szkoła podstawowa/Zadania testowe/Zadania z treścią/Geometryczne

Zadanie nr 5761124

Czy stół, którego blat ma kształt koła o polu 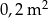2 0,2 m można zakryć prostokątnym obrusem o szerokości 50 cm i długości 75 cm?
Wybierz odpowiedź T (tak) albo N (nie) i jej uzasadnienie spośród oznaczonych literami A–D.

TakNie
ponieważ
A) średnica stołu jest mniejsza od przekątnej prostokąta.
B) średnica stołu jest mniejsza od każdego z boków prostokąta.
C) średnica stołu jest większa od przekątnej prostokąta.
D) średnica stołu jest większa od jednego z boków prostokąta.
Wersja PDF

Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

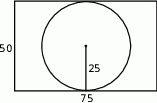
Widać, że największy okrągły stół jaki może przykryć ten obrus ma promień 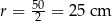r = 502-= 25 cm . Pole powierzchni takiego stołu jest równe

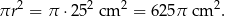
πr 2 = π ⋅2 52 cm 2 = 62 5π cm 2.

Sprawdźmy teraz, czy pole to jest nie mniejsze niż od 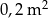0,2 m 2 . Sprawdzamy, czy spełniona jest nierówność

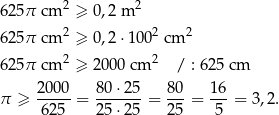
625π cm 2 ≥ 0,2 m 2 2 2 2 625π cm ≥ 0,2⋅10 0 cm 625π cm 2 ≥ 2000 cm 2 / : 62 5 cm π ≥ 2000-= 80-⋅25-= 80-= 16-= 3 ,2 . 62 5 25 ⋅25 25 5

Ponieważ 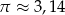π ≈ 3,14 powyższa nierówność nie jest prawdziwa, więc obrus jest za mały, aby przykryć stół o polu 0 ,2 m 2 .  
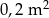Odpowiedź: N, D

Wersja PDF