Oblicz 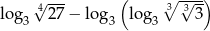 .
.
/Szkoła średnia/Liczby
Oblicz 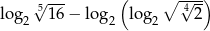 .
.
Oblicz wartość wyrażenia 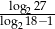 .
.
Zapisz wyrażenie w prostszej postaci 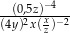 .
.
Wiadomo, że 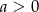 i
i 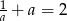 . Wykaż, że
. Wykaż, że 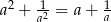 .
.
Uzasadnij, że jeżeli  jest liczbą rzeczywistą różną od zera i
jest liczbą rzeczywistą różną od zera i 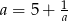 , to
, to 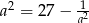 .
.
Uzasadnij, że jeżeli  jest liczbą rzeczywistą różną od zera i
jest liczbą rzeczywistą różną od zera i 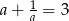 , to
, to 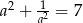 .
.
Wykaż, że liczba 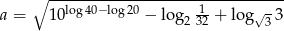 jest liczbą naturalną.
jest liczbą naturalną.
Uzasadnij, że jeśli 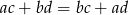 to
to 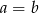 lub
lub 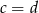 .
.
Wykaż, że jeżeli 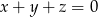 to zachodzi równość
to zachodzi równość
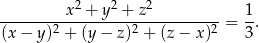
Wykaż, że jeśli 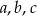 są dowolnymi liczbami rzeczywistymi takimi, że
są dowolnymi liczbami rzeczywistymi takimi, że 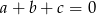 , to
, to
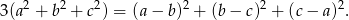
Wykaż, że jeżeli liczby rzeczywiste 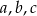 spełniają warunek
spełniają warunek 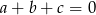 , to
, to
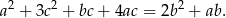
Wykaż, że dla każdej liczby całkowitej  liczba
liczba 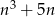 jest podzielna przez 6.
jest podzielna przez 6.
Wykaż, że dla każdej liczby naturalnej  liczba
liczba 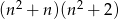 jest podzielna przez 6.
jest podzielna przez 6.
Wykaż, że dla każdej liczby naturalnej  liczba
liczba 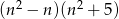 jest podzielna przez 6.
jest podzielna przez 6.
Udowodnij, że jeśli 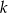 i
i  są liczbami naturalnymi oraz
są liczbami naturalnymi oraz 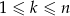 , to
, to 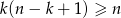 .
.
Wykaż, że jeżeli 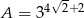 i
i 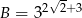 , to
, to 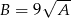 .
.
Wykaż, że jeżeli 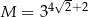 i
i 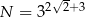 , to
, to 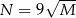 .
.
Suma dwóch liczb jest równa 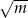 , a ich różnica jest równa
, a ich różnica jest równa 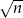 , gdzie
, gdzie 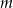 i
i  są dodatnimi liczbami całkowitymi. Wykaż, że iloczyn tych liczb jest liczbą wymierną.
są dodatnimi liczbami całkowitymi. Wykaż, że iloczyn tych liczb jest liczbą wymierną.
Liczby rzeczywiste 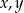 spełniają warunki:
spełniają warunki: 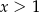 ,
, 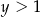 oraz
oraz 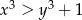 . Wykaż, że prawdziwa jest równość
. Wykaż, że prawdziwa jest równość
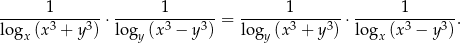
Udowodnij, że suma sześcianów trzech kolejnych liczb naturalnych jest podzielna przez 9.
Udowodnij, że suma sześcianów trzech kolejnych liczb całkowitych nieparzystych jest podzielna przez 9.
Udowodnij, że suma sześcianów trzech kolejnych liczb całkowitych niepodzielnych przez 4 jest liczbą podzielną przez 36.
Pokazać, że dla każdej liczby całkowitej  liczba
liczba 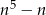 jest podzielna przez 5.
jest podzielna przez 5.
Wykaż, że dla każdej liczby całkowitej  liczba
liczba 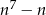 jest podzielna przez 7.
jest podzielna przez 7.
Wykaż, że
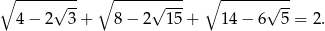
Dla jakich liczb naturalnych  , liczba
, liczba 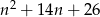 jest kwadratem liczby naturalnej?
jest kwadratem liczby naturalnej?
Dla jakich liczb naturalnych  , liczba
, liczba 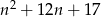 jest kwadratem liczby naturalnej?
jest kwadratem liczby naturalnej?
Wykaż, że równanie 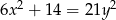 nie ma rozwiązań całkowitych.
nie ma rozwiązań całkowitych.
Uzasadnij, że dla dowolnej liczby naturalnej 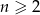 spełniona jest równość
spełniona jest równość
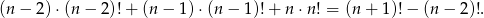
Udowodnij, że 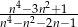 , dla
, dla 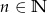 i
i 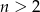 jest ułamkiem właściwym.
jest ułamkiem właściwym.

