/Szkoła średnia/Zadania maturalne/Matura 2013/Matura próbna
Próbny Egzamin Maturalny
z Matematyki (CEN Bydgoszcz)
poziom rozszerzony 4 lutego 2013 Czas pracy: 180 minut
Rozwiąż równanie 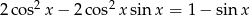 w przedziale
w przedziale 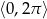 .
.
Dany jest czworokąt 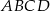 . Niech
. Niech 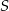 będzie punktem przecięcia jego przekątnych. Udowodnij, że czworokąt
będzie punktem przecięcia jego przekątnych. Udowodnij, że czworokąt 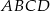 można wpisać w okrąg wtedy i tylko wtedy, gdy
można wpisać w okrąg wtedy i tylko wtedy, gdy 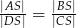 .
.
Dane są funkcje 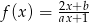 oraz
oraz 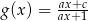 , o których wiadomo, że ich wykresy mają punkt wspólny
, o których wiadomo, że ich wykresy mają punkt wspólny 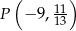 , a miejscem zerowym funkcji
, a miejscem zerowym funkcji 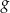 jest liczba:
jest liczba: 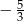 . Wyznacz wartości parametrów
. Wyznacz wartości parametrów 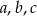 .
.
Narysuj wykres funkcji 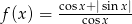 dla
dla 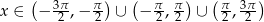 . Podaj zbiór rozwiązań nierówności
. Podaj zbiór rozwiązań nierówności 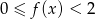 .
.
Suma trzech liczb będących kolejnymi wyrazami rosnącego ciągu geometrycznego jest równa 52. Jeżeli do pierwszej liczby dodamy 2, do drugiej 12, a do trzeciej 6, to otrzymamy trzy kolejne wyrazy ciągu arytmetycznego. Wyznacz ten ciąg.
Podstawą ostrosłupa jest trójkąt, którego jeden z boków ma długość 6, a kąty przyległe do niego mają miary 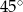 i
i 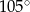 . Wysokość ostrosłupa ma długość równą długości promienia okręgu opisanego na podstawie. Oblicz objętość ostrosłupa. Wynik podaj w postaci
. Wysokość ostrosłupa ma długość równą długości promienia okręgu opisanego na podstawie. Oblicz objętość ostrosłupa. Wynik podaj w postaci 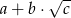 , gdzie
, gdzie  ,
, 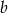 ,
,  są liczbami wymiernymi.
są liczbami wymiernymi.
Dany jest wielomian 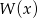 stopnia
stopnia 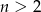 , którego suma wszystkich współczynników jest równa 4, a suma współczynników przy potęgach o wykładnikach nieparzystych jest równa sumie współczynników przy potęgach o wykładnikach parzystych. Wykaż, że reszta
, którego suma wszystkich współczynników jest równa 4, a suma współczynników przy potęgach o wykładnikach nieparzystych jest równa sumie współczynników przy potęgach o wykładnikach parzystych. Wykaż, że reszta 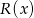 z dzielenia tego wielomianu przez wielomian
z dzielenia tego wielomianu przez wielomian 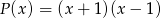 jest równa
jest równa 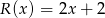 .
.
Narysuj wykres funkcji 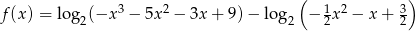 .
.
Ze zbioru liczb 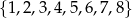 wybieramy losowo jednocześnie cztery liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że najmniejszą wylosowaną liczbą będzie 3 lub największą wylosowaną liczbą będzie 7.
wybieramy losowo jednocześnie cztery liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że najmniejszą wylosowaną liczbą będzie 3 lub największą wylosowaną liczbą będzie 7.
Punkty 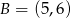 i
i 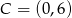 są wierzchołkami trapezu równoramiennego
są wierzchołkami trapezu równoramiennego 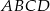 , którego podstawy
, którego podstawy 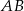 i
i 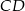 są prostopadłe do prostej
są prostopadłe do prostej 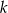 o równaniu
o równaniu 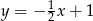 . Oblicz współrzędne pozostałych wierzchołków trapezu, wiedząc, że punkt
. Oblicz współrzędne pozostałych wierzchołków trapezu, wiedząc, że punkt 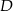 należy do prostej
należy do prostej 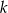 .
.
Wykaż, że dla dowolnych liczb rzeczywistych 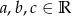 zachodzi nierówność
zachodzi nierówność
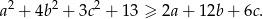
W trapezie opisanym na okręgu boki nierównoległe mają długości 3 i 5, zaś odcinek łączący środki tych boków dzieli trapez na dwie części, których pola są w stosunku 5:11. Oblicz długości podstaw trapezu.

