/Szkoła średnia/Zadania maturalne/Matura 2013/Matura próbna/CKE, OKE, CEN
Lubelska próba przed maturą
z matematyki (dla klas pierwszych)
poziom podstawowy grupa II 6 czerwca 2012 Czas pracy: 170 minut
Zadania zamknięte
Trzecia część liczby 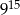 wynosi
wynosi
A) 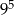 B)
B) 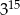 C)
C) 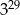 D)
D) 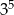
Przedstaw wyrażenie 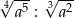 w postaci jednej potęgi
w postaci jednej potęgi
A) 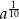 B)
B) 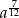 C)
C) 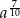 D)
D) 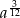
Która z liczb jest największa?
A) 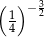 B)
B) 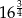 C)
C) 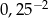 D)
D) 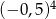
Kwadratem liczby 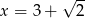 jest
jest
A) 11 B) 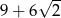 C)
C) 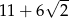 D)
D) 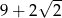
Równanie 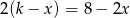 z niewiadomą
z niewiadomą  ma nieskończenie wiele rozwiązań dla
ma nieskończenie wiele rozwiązań dla
A) 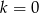 B)
B) 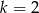 C)
C) 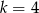 D)
D) 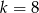
Dziedziną funkcji 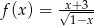 jest
jest
A) 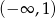 B)
B) 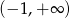 C)
C) 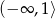 D)
D) 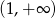
Liczba 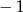 jest miejscem zerowym funkcji
jest miejscem zerowym funkcji 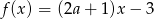 . Wynika stąd, że
. Wynika stąd, że
A) 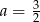 B)
B) 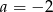 C)
C) 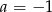 D)
D) 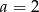
Miara kąta  jest równa:
jest równa:
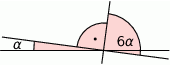
A) 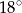 B)
B) 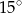 C)
C) 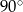 D)
D) 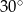
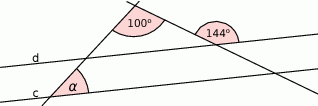
Wiedząc, że 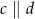 podaj miarę kąta
podaj miarę kąta  .
.
A) 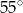 B)
B) 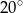 C)
C) 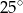 D)
D) 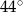
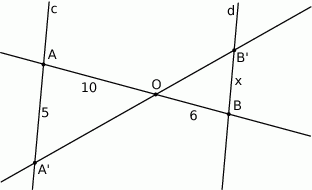
Proste  i
i  są równoległe. Jaką długość ma odcinek
są równoległe. Jaką długość ma odcinek  ?
?
A) 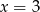 B)
B) 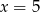 C)
C) 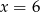 D)
D) 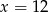
Jakie jest wzajemne położenie okręgów 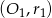 i
i 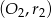 jeżeli wiadomo, że:
jeżeli wiadomo, że: 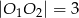 ,
, 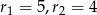
A) przecinające się
B) rozłączne wewnętrznie
C) współśrodkowe
D) rozłączne zewnętrznie
Długość każdego boku kwadratu zwiększono o 20%. Wtedy pole tego kwadratu:
A) wzrośnie o 44% B) wzrośnie o 20% C) wzrośnie dwukrotnie D) wzrośnie o 40%
Które z podanych równań nie ma rozwiązania:
A) 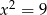 B)
B) 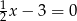 C)
C) 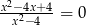 D)
D) 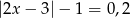
Liczbą odwrotną do liczby 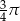 jest liczba:
jest liczba:
A) 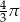 B)
B) 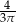 C)
C) 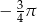 D)
D) 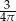
Zbiorem rozwiązań nierówności 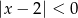 jest
jest
A) 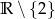 B)
B) 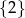 C)
C) 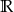 D)
D) 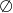
Wyrażenie 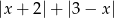 dla
dla 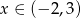 jest równe:
jest równe:
A) 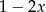 B)
B) 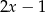 C) 5 D)
C) 5 D) 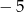
Aby usunąć niewymierność z mianownika ułamka 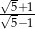 należy mianownik tego ułamka pomnożyć przez:
należy mianownik tego ułamka pomnożyć przez:
A) 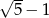 B)
B) 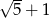 C)
C) 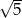 D)
D) 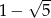
Średnia arytmetyczna zestawu danych: 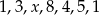 wynosi 4. Wynika z tego, że:
wynosi 4. Wynika z tego, że:
A) 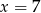 B)
B) 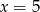 C)
C) 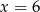 D)
D) 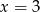
Drut o długości 45 m pocięto na trzy części, których stosunek długości jest równy 2 : 3 : 4. Najkrótsza z tych części ma długość:
A) 10 m B) 15 m C) 5 m D) 20 m
Suma kwadratów długości trzech boków trójkąta prostokątnego jest równa 162. Zatem przeciwprostokątna może mieć długość:
A) 54 B) 9 C) 12 D) 81
Zadania otwarte
Rozwiąż nierówność 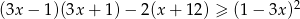 .
.
Dane są liczby: 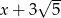 i
i 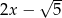 . Wyznacz liczbę
. Wyznacz liczbę 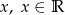 tak, aby liczby te były liczbami przeciwnymi.
tak, aby liczby te były liczbami przeciwnymi.
Udowodnij, że jeżeli liczba 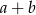 jest różna od zera oraz
jest różna od zera oraz 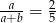 to
to 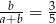 .
.
Wyznacz miejsca zerowe funkcji
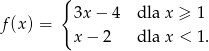
Udowodnij, że liczba 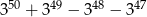 jest podzielna przez 32.
jest podzielna przez 32.
Dany jest trójkąt 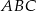 gdzie
gdzie 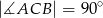 .
.
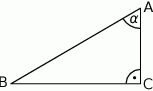
Wiadomo, że 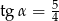 . Podaj wartości pozostałych funkcji trygonometrycznych kąta
. Podaj wartości pozostałych funkcji trygonometrycznych kąta  .
.
Punkty 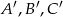 są środkami odpowiednio boków
są środkami odpowiednio boków 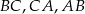 trójkąta
trójkąta 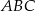 . Uzasadnij, że trójkąt
. Uzasadnij, że trójkąt 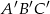 jest przystający do trójkąta
jest przystający do trójkąta 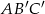 .
.
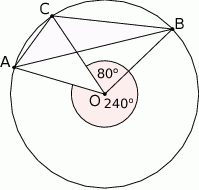
Wyznacz miary kątów trójkąta 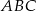 :
:
W poniedziałek cenę pewnego towaru zmniejszono o 10%, zaś w środę zwiększono o 20%. Oblicz początkową cenę tego towaru, jeśli ostatecznie po tych zmianach wynosiła 324 zł.
Różnica dwóch liczb naturalnych dodatnich mniejszych od 130 jest równa 98, a ich największy wspólny dzielnik jest równy 14. Wyznacz te liczby.
Z miast odległych o 45 km o godzinie 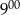 wyjechali naprzeciw siebie dwaj rowerzyści. Każdy z nich jechał ze stałą prędkością. Prędkość jazdy jednego z nich wynosiła 12 km/h. Ile wynosi prędkość jazdy drugiego rowerzysty, jeżeli spotkali się o godzinie
wyjechali naprzeciw siebie dwaj rowerzyści. Każdy z nich jechał ze stałą prędkością. Prędkość jazdy jednego z nich wynosiła 12 km/h. Ile wynosi prędkość jazdy drugiego rowerzysty, jeżeli spotkali się o godzinie 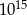 ?
?

