/Studia/Analiza/Ciągi

Zadanie nr 9505103

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz granicę ciągu 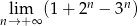n n nl→im+∞ (1+ 2 − 3 ) .

Rozwiązanie

Powinno być jasne, że w podanym wyrażeniu dominuje składnik 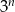n 3 (najszybciej rośnie), zatem granicą powinna być 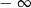− ∞ . Aby to porządnie uzasadnić szacujemy.

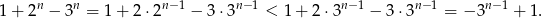
1+ 2n − 3n = 1 + 2 ⋅2n−1 − 3 ⋅3n− 1 < 1+ 2⋅3n −1 − 3⋅3n −1 = − 3n− 1 + 1 .

Ponieważ 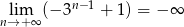n− 1 nl→im+∞(− 3 + 1) = − ∞ , więc taka sama musi być granica danego ciągu.  
Odpowiedź: − ∞

Wersja PDF