Zadanie nr 8410008
Funkcja kwadratowa 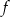 określona jest wzorem
określona jest wzorem 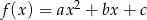 . Zbiorem rozwiązań nierówności
. Zbiorem rozwiązań nierówności 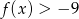 jest przedział
jest przedział 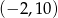 , a zbiorem rozwiązań nierówności
, a zbiorem rozwiązań nierówności 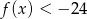 jest zbiór
jest zbiór 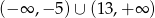 . Oblicz współczynniki
. Oblicz współczynniki 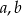 i
i  funkcji
funkcji 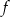 .
.
Rozwiązanie
Zauważmy, że z podanych informacji wynika, że miejscami zerowymi funkcji 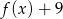 są liczby:
są liczby: 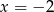 i
i 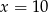 , a miejscami zerowymi funkcji
, a miejscami zerowymi funkcji 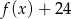 są liczby:
są liczby: 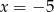 i
i 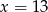 .
.
Sposób I
Z podanych informacji wiemy, że wykresem funkcji 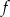 jest parabola o ramionach skierowanych w dół i osi symetrii o równaniu
jest parabola o ramionach skierowanych w dół i osi symetrii o równaniu 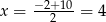 (bo oś symetrii musi przechodzić przez środki podanych zbiorów rozwiązań nierówności). Funkcja
(bo oś symetrii musi przechodzić przez środki podanych zbiorów rozwiązań nierówności). Funkcja 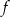 ma więc wzór postaci
ma więc wzór postaci
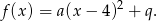
Współczynniki  i
i 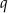 wyznaczymy korzystając z tego, że
wyznaczymy korzystając z tego, że 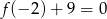 i
i 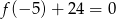 . Mamy więc
. Mamy więc
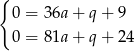
Odejmujemy od drugiego równania pierwsze (żeby skrócić 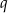 ) i mamy
) i mamy
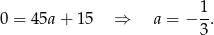
Stąd 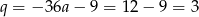 i funkcja
i funkcja 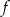 ma wzór
ma wzór
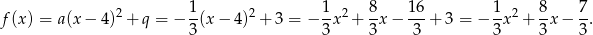
Sposób II
Wiemy, że miejscami zerowymi funkcji 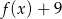 są liczby
są liczby  i
i 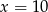 . Zatem
. Zatem
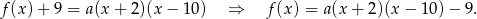
Współczynnik  wyznaczymy korzystając z tego, że
wyznaczymy korzystając z tego, że 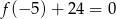
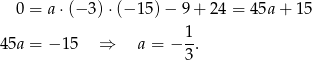
Zatem
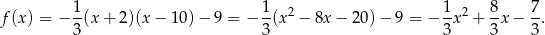
Na koniec wykres funkcji 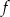 dla ciekawskich.
dla ciekawskich.
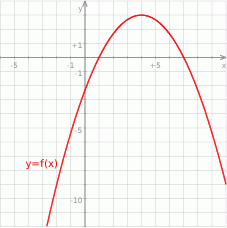
Odpowiedź: