/Szkoła podstawowa/Zadania testowe/Geometria/Trapez

Zadanie nr 2045346

Przekątne trapezu równoramiennego przecinają się pod kątem 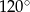∘ 120 i dzielą się w stosunku 2:1. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.

Jeden z kątów trapezu ma miarę 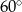∘ 60 . PF
Przekątna dzieli jeden z kątów trapezu w stosunku 3:1.PF
Wersja PDF

Rozwiązanie

Szkicujemy trapez.

PIC

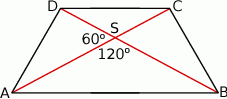
Jeżeli kąt rozwarty między przekątnymi trapezu ma miarę 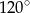1 20∘ , to kąt ostry ma miarę 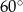60∘ . Wiemy ponadto, że 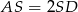AS = 2SD , więc trójkąt 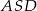ASD jest podobny do połówki trójkąta równobocznego (cecha 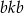bkb ). W szczególności

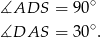
∡ADS = 90∘ ∘ ∡DAS = 30 .

Wiemy też, że trójkąt 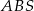ABS jest równoramienny, więc

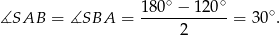
∘ ∘ ∡SAB = ∡SBA = 180--−-1-20- = 30 ∘. 2

Stąd 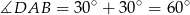∘ ∘ ∘ ∡DAB = 30 + 30 = 60 oraz

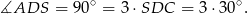
∘ ∘ ∡ADS = 90 = 3 ⋅SDC = 3 ⋅30 .

 
Odpowiedź: P, P

Wersja PDF