/Gimnazjum/Egzamin gimnazjalny/Egzamin 2013/Próbne testy
Próbny Egzamin Gimnazjalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info 13 kwietnia 2013 Czas pracy: 90 minut
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
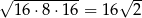 | P | F |
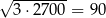 | P | F |
Grupie dwustu osób zadano pytanie: „Jaka jest twoja ulubiona dyscyplina sportu?”. Wyniki tej ankiety przedstawiono na wykresie.
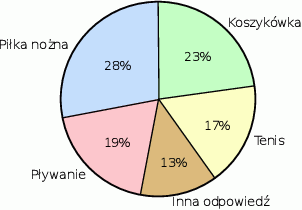
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Z informacji podanych na diagramie wynika, że:
A) 28 osób jako ulubioną dyscyplinę podało piłkę nożną.
B) Łączna liczba odpowiedzi: „piłka nożna” i „tenis” jest równa liczbie wszystkich pozostałych odpowiedzi.
C) Liczba odpowiedzi „pływanie” była o 4 większa od liczby odpowiedzi „tenis”.
D) Liczba odpowiedzi „tenis” była o 6 mniejsza od liczby odpowiedzi „koszykówka”.
Na rysunkach przedstawiono osie liczbowe, a na każdej z nich kropkami zaznaczono siedem liczb.
Na którym rysunku jedna z tych liczb jest medianą pozostałych sześciu liczb? Wybierz odpowiedź spośród podanych.
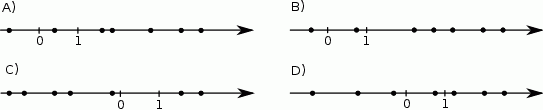
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Liczba 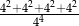 jest równa
jest równa
A) 1 B) 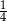 C) 4 D)
C) 4 D) 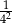
Które zdanie jest prawdziwe? Wybierz odpowiedź spośród podanych.
A) Iloczyn dwóch kolejnych liczb naturalnych jest liczbą parzystą.
B) Iloczyn dwóch kolejnych liczb naturalnych jest liczbą podzielną przez 3.
C) Suma dwóch kolejnych liczb naturalnych jest liczbą parzystą.
D) Suma dwóch kolejnych liczb naturalnych jest liczbą podzielną przez 3.
Dwunastu malarzy pracując z jednakową wydajnością pomalowało burtę statku w ciągu 8 godzin. Ilu malarzy powinno malować tę burtę, aby tę samą pracę wykonać w ciągu 6 godzin? Wybierz odpowiedź spośród podanych.
A) 14 B) 16 C) 18 D) 20
Pani Halina włącza pralkę średnio 5 razy w tygodniu. W trakcie jednego prania średnio zużywa 90 g proszku do prania.
Na ile tygodni wystarczy pani Halinie siedmiokilogramowe opakowanie proszku? Wybierz odpowiedź spośród podanych.
A) 9 B) 12 C) 15 D) 16
Informacja do zadań 8 i 9
W pudełku z cukierkami znajdowało się 80 cukierków w trzech kolorach. Cukierków niebieskich było dwa razy więcej niż cukierków zielonych, a cukierków czerwonych było sześć razy mniej niż cukierków niebieskich.
Jaki procent cukierków stanowiły cukierki niebieskie? Wybierz odpowiedź spośród podanych.
A) 30% B) 60% C) 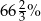 D)
D) 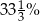
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W pudełku jest o 20 więcej cukierków niebieskich niż zielonych. | P | F |
| W pudełku jest o 20 więcej cukierków zielonych niż czerwonych. | P | F |
Informacja do zadań 10 i 11
Na torze wyścigowym zorganizowano wyścig samochodowy, w którym wzięły udział dwa samochody. Oba samochody wystartowały w tym samym momencie i każdy z nich pokonał dystans 600 km, przy czym do mety jako pierwszy przyjechał samochód nr 2. Wykresy przedstawiają zależność drogi przebytej przez oba samochody od czasu jazdy.
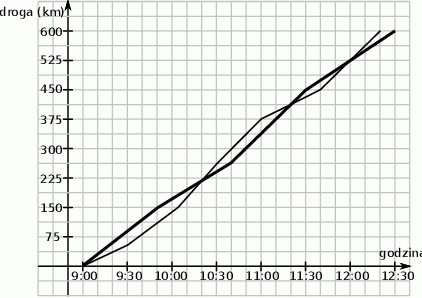
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Po rozpoczęciu wyścigu trzykrotnie następowała zmiana lidera. | P | F |
| Gdyby wyścig zakończył się po 300 km, to wygrałby go samochód nr 1. | P | F |
Dokończ zdanie. Zaznacz dobrą odpowiedź. Średnia prędkość samochodu nr 2 na trasie wyścigu wyniosła
A) 150 km/h B) 171,4 km/h C) 180 km/h D) 190 km/h
W trójkącie 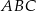 , w którym
, w którym 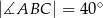 ,
, 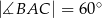 poprowadzono dwusieczne
poprowadzono dwusieczne 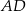 i
i 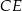 , które przecinają się w punkcie
, które przecinają się w punkcie 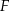 .
.
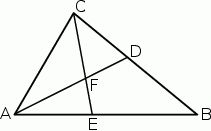
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
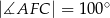 | P | F |
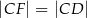 | P | F |
Informacja do zadań 13 i 14
Liczbę ogniw  łańcucha rowerowego można dobrać korzystając ze wzoru
łańcucha rowerowego można dobrać korzystając ze wzoru
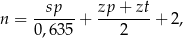
gdzie 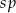 jest odległością w centymetrach od osi suportu do osi tylnej piasty,
jest odległością w centymetrach od osi suportu do osi tylnej piasty, 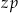 jest liczbą zębów największej zębatki z przodu, a
jest liczbą zębów największej zębatki z przodu, a 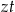 liczbą zębów największej zębatki z tyłu.
liczbą zębów największej zębatki z tyłu.
W tabeli podano niektóre parametry roweru.
| Liczba ogniw łańcucha | 114 |
| Liczba zębów największej zębatki z tyłu | 30 |
| Liczba zębów największej zębatki z przodu | 34 |
Jaka jest odległość osi suportu od osi tylnej piasty w tym rowerze? Wybierz odpowiedź spośród podanych.
A) 50,8 cm B) 48,26 cm C) 46,99 cm D) 45,72 cm
Jacek w swoim rowerze wymienił przednie zębatki tak, że zmniejszył liczbę zębów największej zębatki z 46 do 42 zębów.
Dokończ zdanie wybierając odpowiedź spośród podanych.
Jacek po wymianie zębatek powinien skrócić łańcuch o
A) 1 ogniwo B) 2 ogniwa C) 3 ogniwa D) 4 ogniwa
W prostokątnym układzie współrzędnych umieszczone są dwa przystające trójkąty oraz prosta 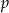 tak, jak na rysunku.
tak, jak na rysunku.
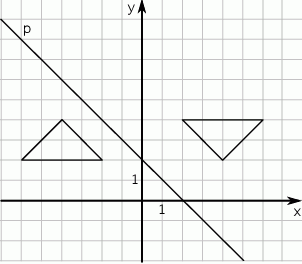
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Jeden trójkąt jest symetryczny do drugiego względem
A) osi 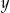 B) prostej
B) prostej 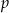
C) punktu 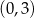 D) punktu przecięcia prostej
D) punktu przecięcia prostej 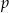 i osi
i osi 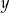 .
.
W jakim stosunku można podzielić odcinek o długości 24 cm, aby z otrzymanych trzech odcinków zbudować trójkąt równoramienny? Wybierz odpowiedź spośród podanych.
A) 2 : 2 : 6 B) 2 : 3 : 4 C) 3 : 5 : 3 D) 3 : 1 : 1
Dwie proste równoległe 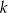 i
i 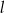 przecięto prostymi
przecięto prostymi 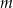 i
i  w sposób przedstawiony na rysunku.
w sposób przedstawiony na rysunku.
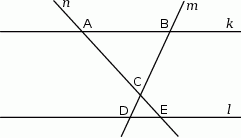
Czy trójkąty 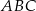 i
i 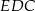 są przystające? Wybierz odpowiedź T albo N oraz jej uzasadnienie spośród zdań oznaczonych literami A–D.
są przystające? Wybierz odpowiedź T albo N oraz jej uzasadnienie spośród zdań oznaczonych literami A–D.
| Tak | Nie |
| ponieważ | |
| A) | te trójkąty mają wspólny wierzchołek. |
| B) | te trójkąty mają boki różnej długości. |
| C) | te trójkąty mają odpowiednie kąty równej miary. |
| D) | te trójkąty mają boki równoległe. |
Kształt i wymiary drewnianej zabawki przedstawiono na rysunku.
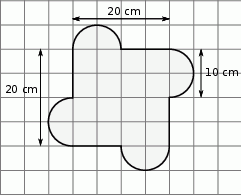
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Powierzchnia tej zabawki (w 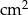 ) jest równa
) jest równa
A) 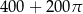 B)
B) 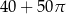 C)
C) 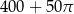 D)
D) 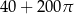
Z 1 000 000 sześcianów o objętości 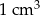 zbudowano prostopadłościan o polu podstawy równym
zbudowano prostopadłościan o polu podstawy równym 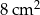 .
.
![]()
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Objętość prostopadłościanu jest równa 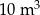 . . | P | F |
| Wysokość prostopadłościanu jest równa 1,25 km. | P | F |
Na rysunku podano wymiary trzech pojemników w kształcie walca.
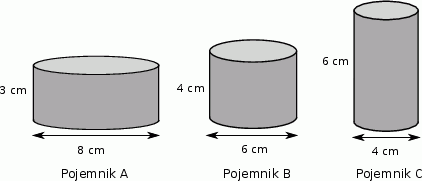
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Objętość pojemnika 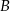 stanowi 70% objętości pojemnika stanowi 70% objętości pojemnika 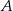 . . | P | F |
Objętość pojemnika 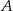 jest dwa razy większa od objętości pojemnika jest dwa razy większa od objętości pojemnika 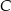 . . | P | F |
Asia napisała na tablicy liczbę trzycyfrową, która jest podzielna przez 45, i w której zapisie występują tylko dwie różne cyfry. Jaką liczbę mogła napisać Asia? Podaj wszystkie możliwości. Odpowiedź uzasadnij.
Pole powierzchni całkowitej ostrosłupa prawidłowego czworokątnego jest równe 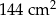 . Pole podstawy tej bryły stanowi 80% pola powierzchni bocznej tego ostrosłupa. Oblicz długość krawędzi podstawy tej bryły. Zapisz obliczenia.
. Pole podstawy tej bryły stanowi 80% pola powierzchni bocznej tego ostrosłupa. Oblicz długość krawędzi podstawy tej bryły. Zapisz obliczenia.
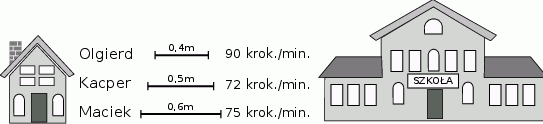
Trzech braci: Olgierd, Kacper i Maciek pokonują tę samą drogę z domu do szkoły. Olgierd stawia kroki długości 0,4 m w tempie 90 kroków na minutę, Kacper stawia kroki długości 0,5 m w tempie 72 kroków na minutę, a Maciek stawia kroki długości 0,6 m w tempie 75 kroków na minutę. Olgierd i Kacper przyszli do szkoły dokładnie w tym samym momencie, przy czym Kacper zrobił 900 kroków mniej od Olgierda. Oblicz, ile minut zajmie droga do szkoły Maćkowi.