Okrąg przecina boki czworokąta 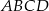 kolejno w punktach
kolejno w punktach 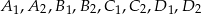 (zobacz rysunek).
(zobacz rysunek).
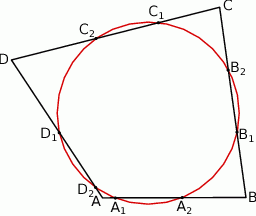
Wykaż, że jeżeli 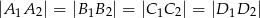 , to w czworokąt
, to w czworokąt 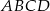 można wpisać okrąg.
można wpisać okrąg.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Okrąg przecina boki czworokąta 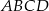 kolejno w punktach
kolejno w punktach 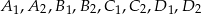 (zobacz rysunek).
(zobacz rysunek).

Wykaż, że jeżeli 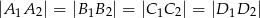 , to w czworokąt
, to w czworokąt 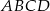 można wpisać okrąg.
można wpisać okrąg.
Kąt ostry między przekątnymi równoległoboku 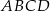 ma miarę
ma miarę 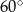 . Przekątna
. Przekątna 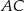 ma długość 6, a przekątna
ma długość 6, a przekątna 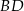 jest prostopadła do boku
jest prostopadła do boku 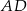 . Oblicz długości boków równoległoboku.
. Oblicz długości boków równoległoboku.
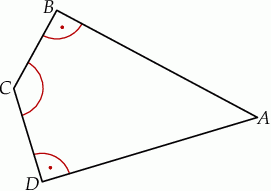
W czworokącie wypukłym 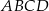 (zobacz rysunek poniżej) dane są kąty:
(zobacz rysunek poniżej) dane są kąty: 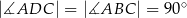 oraz
oraz 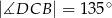 . Wykaż, że
. Wykaż, że 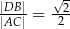 .
.
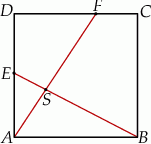
Na bokach 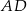 i
i 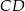 kwadratu
kwadratu 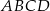 o boku długości 1 wybrano punkty
o boku długości 1 wybrano punkty 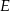 i
i 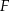 w ten sposób, że
w ten sposób, że 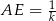 i
i 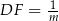 , dla
, dla 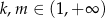 . Niech
. Niech 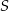 będzie punktem przecięcia odcinków
będzie punktem przecięcia odcinków 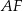 i
i 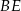
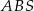 jest prostokątny to
jest prostokątny to 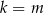 .
. 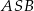 jeżeli
jeżeli 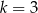 i
i 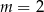 .
.Dany jest trapez prostokątny 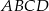 o podstawach
o podstawach 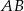 i
i 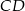 , w którym boki
, w którym boki 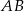 i
i 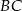 są prostopadłe. Dwusieczne kątów
są prostopadłe. Dwusieczne kątów 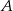 i
i 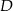 przecinają się w punkcie
przecinają się w punkcie 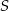 leżącym na boku
leżącym na boku 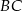 . Wykaż, że
. Wykaż, że 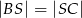 .
.
Ramię trapezu równoramiennego 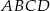 ma długość
ma długość 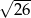 . Przekątne w tym trapezie są prostopadłe, a punkt ich przecięcia dzieli je w stosunku 2:3. Oblicz pole tego trapezu.
. Przekątne w tym trapezie są prostopadłe, a punkt ich przecięcia dzieli je w stosunku 2:3. Oblicz pole tego trapezu.
Dany jest prostokąt o polu 12, w którym długość przekątnej jest liczbą z przedziału 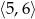 . Wykaż, że obwód tego prostokąta jest liczbą z przedziału
. Wykaż, że obwód tego prostokąta jest liczbą z przedziału 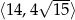 .
.
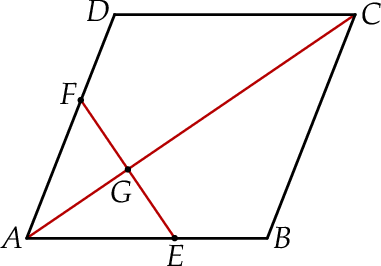
Na bokach 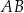 i
i 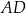 rombu
rombu 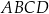 wybrano odpowiednio punkty
wybrano odpowiednio punkty 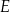 i
i 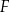 tak, że
tak, że 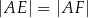 . Pole pięciokąta
. Pole pięciokąta 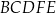 jest 17 razy większe niż pole trójkąta
jest 17 razy większe niż pole trójkąta 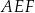 . Punkt
. Punkt 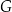 jest punktem wspólnym odcinka
jest punktem wspólnym odcinka 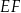 i przekątnej
i przekątnej 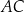 . Oblicz Oblicz
. Oblicz Oblicz 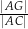 .
.
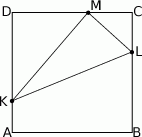
Na bokach 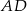 ,
, 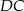 i
i 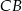 kwadratu
kwadratu 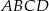 wybrano punkty
wybrano punkty 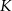 ,
, 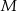 i
i 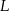 ten sposób, że
ten sposób, że 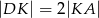 ,
, 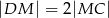 , oraz
, oraz 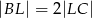 .
.
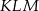 jest prostokątny.
jest prostokątny. 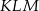 .
.
Pole rombu jest równe 120. Gdyby zwiększyć długości jego przekątnych odpowiednio o 2 i 5 to pole wzrosłoby o 55. Oblicz obwód rombu. Podaj wszystkie możliwe odpowiedzi.
W prostokąt wpisano trzy parami styczne okręgi w ten sposób, że dwa z nich są styczne do trzech boków, prostokąta, a trzeci jest styczny do jednego z boków prostokąta (patrz rysunek). Oblicz promień mniejszego okręgu jeżeli promień większego okręgu jest równy 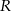 .
.
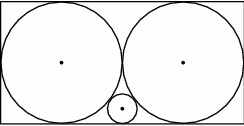
Przekątne czworokąta 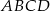 są prostopadłe. Wykaż, że
są prostopadłe. Wykaż, że 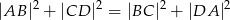 .
.
Dany jest czworokąt wypukły 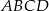 niebędący równoległobokiem. Punkty
niebędący równoległobokiem. Punkty 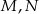 są odpowiednio środkami boków
są odpowiednio środkami boków 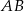 i
i 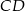 . Punkty
. Punkty 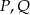 są odpowiednio środkami przekątnych
są odpowiednio środkami przekątnych 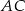 i
i 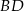 . Uzasadnij, że
. Uzasadnij, że 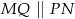 .
.
Dany jest czworokąt wypukły 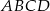 niebędący równoległobokiem. Punkty
niebędący równoległobokiem. Punkty 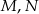 są odpowiednio środkami boków
są odpowiednio środkami boków 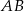 i
i 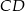 . Punkty
. Punkty 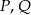 są odpowiednio środkami przekątnych
są odpowiednio środkami przekątnych 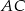 i
i 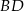 . Uzasadnij, że czworokąt
. Uzasadnij, że czworokąt 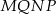 jest równoległobokiem.
jest równoległobokiem.
W prostokącie 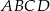 , w którym stosunek długości boków
, w którym stosunek długości boków 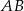 i
i 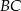 jest równy 4:3, poprowadzono dwusieczne kątów
jest równy 4:3, poprowadzono dwusieczne kątów 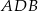 i
i 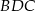 . Dwusieczne te przecinają boki
. Dwusieczne te przecinają boki 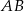 i
i 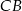 odpowiednio w punktach
odpowiednio w punktach 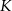 i
i 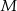 . Oblicz stosunek pola prostokąta
. Oblicz stosunek pola prostokąta 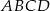 do pola trójkąta
do pola trójkąta 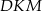 .
.
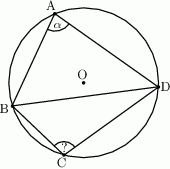
Wszystkie wierzchołki czworokąta 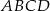 leżą na okręgu oraz
leżą na okręgu oraz 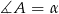 . Oblicz miarę kąta
. Oblicz miarę kąta 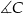 .
.
W okrąg o promieniu 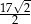 wpisano czworokąt
wpisano czworokąt 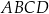 tak, że
tak, że 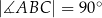 oraz
oraz 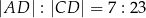 . Oblicz obwód czworokąta
. Oblicz obwód czworokąta 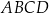 jeżeli jego pole jest równe 192.
jeżeli jego pole jest równe 192.
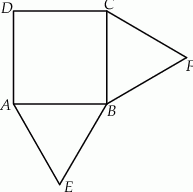
Na zewnątrz kwadratu 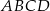 na bokach
na bokach 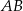 i
i 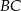 zbudowano trójkąty równoboczne
zbudowano trójkąty równoboczne 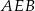 i
i 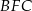 . Uzasadnij, że trójkąt
. Uzasadnij, że trójkąt 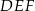 jest równoboczny.
jest równoboczny.
Długość ramienia trapezu jest równa 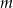 , a odległość od niego środka przeciwległego ramienia jest równa
, a odległość od niego środka przeciwległego ramienia jest równa 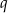 . Wyznacz pole trapezu.
. Wyznacz pole trapezu.
W kole o promieniu 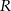 poprowadzono średnicę
poprowadzono średnicę 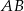 i równoległą do niej cięciwę
i równoległą do niej cięciwę 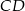 . Oblicz pole powstałego trapezu
. Oblicz pole powstałego trapezu 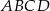 , jeżeli kąt ostry tego trapezu ma miarę
, jeżeli kąt ostry tego trapezu ma miarę  .
.
Różnica kwadratów długości przekątnych trapezu prostokątnego wynosi 21, jego wysokość ma długość 4, a dłuższe ramię ma długość 5. Oblicz pole trapezu.
