Przeciwległe boki czworokąta 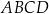 wpisanego w okrąg przecinają się w punktach
wpisanego w okrąg przecinają się w punktach 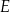 i
i 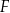 (zobacz rysunek), przy czym odcinek
(zobacz rysunek), przy czym odcinek 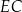 jest zawarty w dwusiecznej kąta
jest zawarty w dwusiecznej kąta 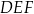 , a odcinek
, a odcinek 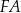 jest zawarty w dwusiecznej kąta
jest zawarty w dwusiecznej kąta 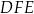 . Wykaż, że
. Wykaż, że 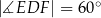 .
.

 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Przeciwległe boki czworokąta 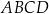 wpisanego w okrąg przecinają się w punktach
wpisanego w okrąg przecinają się w punktach 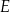 i
i 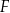 (zobacz rysunek), przy czym odcinek
(zobacz rysunek), przy czym odcinek 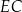 jest zawarty w dwusiecznej kąta
jest zawarty w dwusiecznej kąta 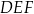 , a odcinek
, a odcinek 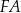 jest zawarty w dwusiecznej kąta
jest zawarty w dwusiecznej kąta 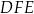 . Wykaż, że
. Wykaż, że 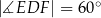 .
.

W trapez prostokątny można wpisać okrąg. Jedna z jego podstaw ma długość  , druga jest trzy razy dłuższa. Oblicz pole trapezu oraz długość odcinka łączącego środki ramion trapezu.
, druga jest trzy razy dłuższa. Oblicz pole trapezu oraz długość odcinka łączącego środki ramion trapezu.
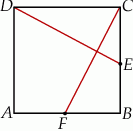
Na rysunku przedstawiono kwadrat 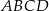 . Punkty
. Punkty 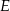 i
i 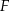 są środkami boków
są środkami boków 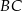 i
i 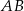 . Uzasadnij, że odcinki
. Uzasadnij, że odcinki 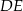 i
i 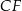 są prostopadłe.
są prostopadłe.
Punkt 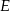 jest środkiem boku
jest środkiem boku 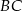 prostokąta
prostokąta 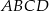 , w którym
, w którym 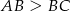 . Punkt
. Punkt 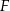 leży na boku
leży na boku 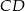 tego prostokąta oraz
tego prostokąta oraz 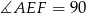 . Udowodnij, że
. Udowodnij, że 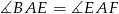 .
.
Dany jest prostokąt o polu 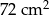 . Gdyby zwiększyć długość jednego z boków o 2 cm, a drugi bok zmniejszyć o 3 cm, to pole nie ulegnie zmianie. Oblicz długości boków danego prostokąta.
. Gdyby zwiększyć długość jednego z boków o 2 cm, a drugi bok zmniejszyć o 3 cm, to pole nie ulegnie zmianie. Oblicz długości boków danego prostokąta.
Dany jest prostokąt o polu 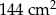 . Gdyby zwiększyć długość jednego z boków o 8 cm, a drugi bok zmniejszyć o 3 cm, to pole nie ulegnie zmianie. Oblicz długości boków danego prostokąta.
. Gdyby zwiększyć długość jednego z boków o 8 cm, a drugi bok zmniejszyć o 3 cm, to pole nie ulegnie zmianie. Oblicz długości boków danego prostokąta.
Przekątne trapezu 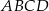 przecinają się w punkcie
przecinają się w punkcie 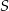 , jego podstawy mają długości
, jego podstawy mają długości 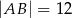 i
i 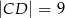 , a wysokość trapezu ma długość 8. Punkt
, a wysokość trapezu ma długość 8. Punkt 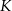 jest środkiem odcinka
jest środkiem odcinka 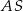 (zobacz rysunek).
(zobacz rysunek).
Oblicz pole trójkąta 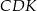 .
.
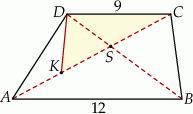
Krótsza podstawa trapezu ma długość 2, a ramiona długości 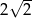 i 4 tworzą z dłuższą podstawą kąty o miarach
i 4 tworzą z dłuższą podstawą kąty o miarach 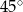 i
i 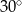 . Oblicz pole trapezu.
. Oblicz pole trapezu.
Krótsza podstawa trapezu ma długość 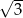 , a ramiona długości
, a ramiona długości 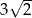 i 6 tworzą z dłuższą podstawą kąty o miarach
i 6 tworzą z dłuższą podstawą kąty o miarach 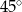 i
i 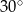 odpowiednio. Oblicz pole trapezu.
odpowiednio. Oblicz pole trapezu.
Długości boków równoległoboku 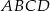 wynoszą 1 i
wynoszą 1 i 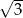 , a kąt przy wierzchołku
, a kąt przy wierzchołku 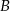 ma miarę
ma miarę 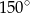 . Oblicz promień okręgu opisanego na trójkącie
. Oblicz promień okręgu opisanego na trójkącie 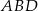 .
.
O ile procent zmniejszy się pole rombu, jeśli jedną przekątną rombu zwiększymy o 20%, a drugą przekątną skrócimy o 40%?
Dwusieczne czworokąta 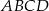 wpisanego w okrąg przecinają się w czterech różnych punktach:
wpisanego w okrąg przecinają się w czterech różnych punktach: 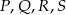 (zobacz rysunek).
(zobacz rysunek).
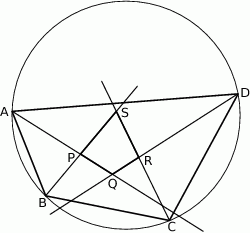
Wykaż, że na czworokącie 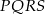 można opisać okrąg.
można opisać okrąg.
Z wierzchołków czworokąta 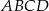 poprowadzono półproste, które przecinają się w wierzchołkach czworokąta
poprowadzono półproste, które przecinają się w wierzchołkach czworokąta 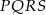 wpisanego w okrąg (zobacz rysunek).
wpisanego w okrąg (zobacz rysunek).
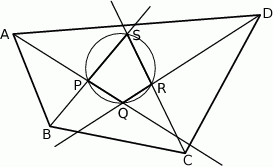
Wykaż, że jeżeli półproste 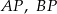 i
i 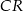 są dwusiecznymi odpowiednio kątów
są dwusiecznymi odpowiednio kątów 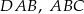 i
i 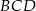 , to półprosta
, to półprosta 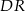 jest dwusieczną kąta
jest dwusieczną kąta 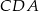 .
.
Dany jest prostokąt 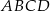 , którego jeden bok jest dwa razy dłuższy od drugiego. Na boku
, którego jeden bok jest dwa razy dłuższy od drugiego. Na boku 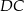 zbudowano trójkąt równoboczny
zbudowano trójkąt równoboczny 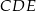 (zobacz rysunek). Punkt
(zobacz rysunek). Punkt 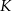 jest takim punktem odcinka
jest takim punktem odcinka 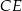 , że
, że 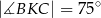 . Udowodnij, że punkt
. Udowodnij, że punkt 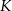 jest środkiem odcinka
jest środkiem odcinka 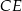 .
.
Długości boków czworokąta 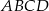 są równe:
są równe: 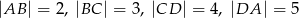 . Na czworokącie
. Na czworokącie 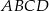 opisano okrąg. Oblicz długość przekątnej
opisano okrąg. Oblicz długość przekątnej 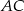 tego czworokąta.
tego czworokąta.
Długości boków czworokąta 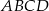 są równe:
są równe: 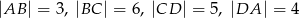 . Na czworokącie
. Na czworokącie 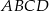 opisano okrąg. Oblicz długość przekątnej
opisano okrąg. Oblicz długość przekątnej 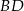 tego czworokąta.
tego czworokąta.
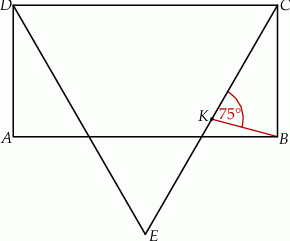
Dany jest trapez prostokątny (zobacz rysunek).
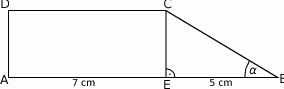
Wyznacz obwód tego trapezu, jeżeli miara kąta przy wierzchołku 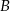 wynosi
wynosi 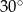 .
.
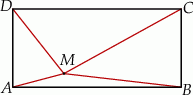
Punkt 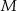 leży wewnątrz prostokąta
leży wewnątrz prostokąta 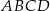 (zob. rysunek). Udowodnij, że
(zob. rysunek). Udowodnij, że 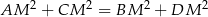 .
.
Dany jest kwadrat 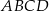 . Przekątne
. Przekątne 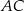 i
i 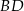 przecinają się w punkcie
przecinają się w punkcie 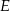 . Punkty
. Punkty 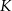 i
i 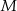 są środkami odcinków – odpowiednio –
są środkami odcinków – odpowiednio – 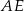 i
i 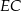 . Punkty
. Punkty 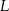 i
i 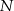 leżą na przekątnej
leżą na przekątnej 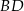 tak, że
tak, że 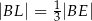 i
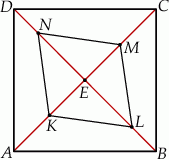
i 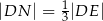 (zobacz rysunek). Wykaż, że stosunek pola czworokąta
(zobacz rysunek). Wykaż, że stosunek pola czworokąta 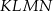 do pola kwadratu
do pola kwadratu 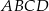 jest równy 1:3.
jest równy 1:3.
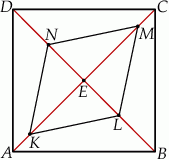
Dany jest kwadrat 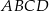 . Przekątne
. Przekątne 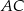 i
i 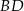 przecinają się w punkcie
przecinają się w punkcie 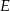 . Punkty
. Punkty 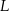 i
i 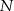 są środkami odcinków – odpowiednio –
są środkami odcinków – odpowiednio – 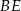 i
i 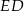 . Punkty
. Punkty 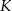 i
i 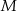 leżą na przekątnej
leżą na przekątnej 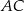 tak, że
tak, że 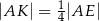 i
i 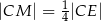 (zobacz rysunek). Wykaż, że stosunek pola czworokąta
(zobacz rysunek). Wykaż, że stosunek pola czworokąta 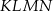 do pola kwadratu
do pola kwadratu 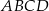 jest równy 3:8.
jest równy 3:8.
Koło i kwadrat mają równe obwody. Wykaż, że pierwsza z tych figur ma większe pole.
Niech  i
i 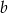 będą długościami kolejnych boków równoległoboku
będą długościami kolejnych boków równoległoboku 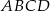 , zaś
, zaś 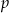 i
i  długościami jego przekątnych. Wykaż, że
długościami jego przekątnych. Wykaż, że 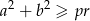 .
.
Wykaż, że jeżeli w czworokącie 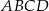 dwusieczne kątów przy wierzchołkach
dwusieczne kątów przy wierzchołkach 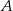 i
i 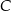 przecinają dwusieczne kątów przy wierzchołkach
przecinają dwusieczne kątów przy wierzchołkach 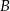 i
i 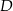 w czterech różnych punktach, to punkty te leżą na pewnym okręgu.
w czterech różnych punktach, to punkty te leżą na pewnym okręgu.
W trójkącie równoramiennym dane są długości podstawy 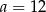 cm i wysokości
cm i wysokości 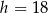 cm. W trójkąt ten wpisano prostokąt w ten sposób, że dwa wierzchołki prostokąta leżą na podstawie, a po jednym na każdym ramieniu trójkąta, przy czym przekątne prostokąta są równoległe do ramion trójkąta. Oblicz długości boków prostokąta.
cm. W trójkąt ten wpisano prostokąt w ten sposób, że dwa wierzchołki prostokąta leżą na podstawie, a po jednym na każdym ramieniu trójkąta, przy czym przekątne prostokąta są równoległe do ramion trójkąta. Oblicz długości boków prostokąta.
W czworokącie wypukłym 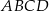 poprowadzono przekątną
poprowadzono przekątną 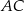 . Okręgi wpisane w trójkąty
. Okręgi wpisane w trójkąty 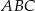 i
i 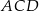 są styczne zewnętrznie. Wykaż, że w czworokąt
są styczne zewnętrznie. Wykaż, że w czworokąt 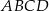 można wpisać okrąg.
można wpisać okrąg.
