Oblicz sumę długości przekątnych rombu wiedząc, że suma ich kwadratów jest równa 313, a pole rombu jest równe 78.
/Szkoła średnia/Geometria/Planimetria/Czworokąt
Romb o kącie ostrym 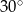 jest opisany na okręgu o promieniu 2. Oblicz pole tego rombu.
jest opisany na okręgu o promieniu 2. Oblicz pole tego rombu.
W romb o boku  wpisano dwa okręgi w ten sposób, że okręgi te są styczne zewnętrznie i każdy z nich jest styczny do dwóch sąsiednich boków rombu przecinających się pod kątem ostrym
wpisano dwa okręgi w ten sposób, że okręgi te są styczne zewnętrznie i każdy z nich jest styczny do dwóch sąsiednich boków rombu przecinających się pod kątem ostrym  (zobacz rysunek).
(zobacz rysunek).
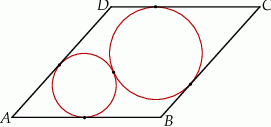
Udowodnij, że suma promieni tych okręgów jest równa 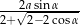 .
.
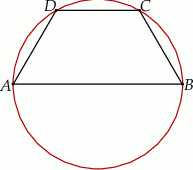
W okrąg wpisano trapez równoramienny 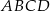 w ten sposób, że podstawa
w ten sposób, że podstawa  jest średnicą tego okręgu. Ramię trapezu ma długość 10, a jego przekątna jest o 11 dłuższa od promienia okręgu. Oblicz wysokość tego trapezu.
jest średnicą tego okręgu. Ramię trapezu ma długość 10, a jego przekątna jest o 11 dłuższa od promienia okręgu. Oblicz wysokość tego trapezu.
Znajdź długości przekątnych rombu o boku 29 jeżeli wiadomo, że ich różnica długości jest równa 2.
W trapezie  o podstawach
o podstawach  i
i 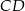 przekątne
przekątne 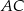 oraz
oraz 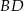 przecinają się w punkcie
przecinają się w punkcie 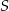 . Wykaż, że jeżeli
. Wykaż, że jeżeli 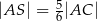 , to pole trójkąta
, to pole trójkąta 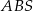 jest 25 razy większe od pola trójkąta
jest 25 razy większe od pola trójkąta 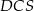 .
.
W trapezie 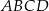 o podstawach
o podstawach 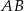 i
i 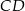 przekątne
przekątne 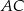 oraz
oraz 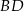 przecinają się w punkcie
przecinają się w punkcie 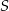 . Wykaż, że jeżeli
. Wykaż, że jeżeli 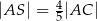 , to pole trójkąta
, to pole trójkąta 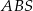 jest 16 razy większe od pola trójkąta
jest 16 razy większe od pola trójkąta 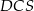 .
.
Wyprowadź wzór na pole trapezu ze wzorów na pole równoległoboku i trójkąta.
W trapezie kąty przy dłuższej podstawie to 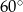 i
i 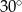 , a długość wysokości trapezu wynosi 6. Oblicz pole trapezu oraz długości jego podstaw wiedząc, że suma długości ramion jest równa sumie długości podstaw.
, a długość wysokości trapezu wynosi 6. Oblicz pole trapezu oraz długości jego podstaw wiedząc, że suma długości ramion jest równa sumie długości podstaw.
Odcinek 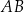 jest dłuższą podstawą trapezu równoramiennego
jest dłuższą podstawą trapezu równoramiennego 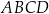 opisanego na okręgu o środku
opisanego na okręgu o środku 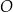 . Oblicz pole tego trapezu jeżeli
. Oblicz pole tego trapezu jeżeli 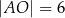 i
i 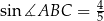 .
.
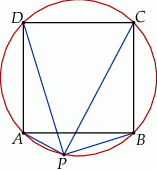
Punkt 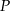 należy do okręgu opisanego na kwadracie
należy do okręgu opisanego na kwadracie 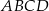 . Wykaż, że
. Wykaż, że 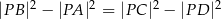 .
.
Prostokąt 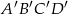 jest podobny do prostokąta
jest podobny do prostokąta 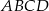 w skali
w skali 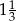 . Pole prostokąta
. Pole prostokąta 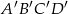 jest równe
jest równe 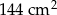 . Krótszy bok prostokąta
. Krótszy bok prostokąta 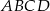 ma długość 6 cm. Oblicz długości pozostałych boków tych prostokątów.
ma długość 6 cm. Oblicz długości pozostałych boków tych prostokątów.
Prostokąt 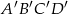 jest podobny do prostokąta
jest podobny do prostokąta 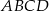 w skali
w skali 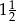 . Pole prostokąta
. Pole prostokąta 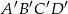 jest równe
jest równe 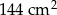 . Krótszy bok prostokąta
. Krótszy bok prostokąta 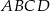 ma długość 9 cm. Oblicz długości pozostałych boków tych prostokątów.
ma długość 9 cm. Oblicz długości pozostałych boków tych prostokątów.
Podstawy trapezu równoramiennego o polu 40 mają długości 6 i 14. Oblicz długość ramienia tego trapezu.
Stosunek długości przekątnych rombu o boku 17 cm jest równy 5:3. Oblicz pole rombu.
Stosunek długości przekątnych rombu o boku 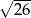 jest równy 3:2. Oblicz pole tego rombu.
jest równy 3:2. Oblicz pole tego rombu.
W równoległoboku 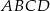 , w którym
, w którym 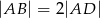 punkt
punkt 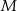 jest środkiem boku
jest środkiem boku 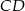 . Wykaż, że trójkąt
. Wykaż, że trójkąt 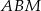 jest prostokątny.
jest prostokątny.
Wierzchołki kwadratu 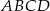 połączono ze środkami jego boków (zobacz rysunek) i otrzymano w ten sposób mniejszy kwadrat
połączono ze środkami jego boków (zobacz rysunek) i otrzymano w ten sposób mniejszy kwadrat 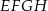 . Oblicz, jaki jest stosunek obwodów kwadratów
. Oblicz, jaki jest stosunek obwodów kwadratów 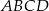 i
i 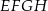 .
.
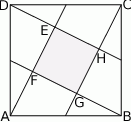
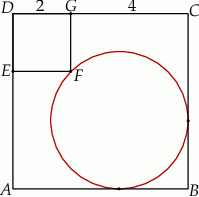
Na rysunku przedstawiono dwa kwadraty: 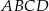 i
i 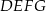 , przy czym punkty
, przy czym punkty 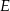 i
i 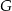 należą do odcinków
należą do odcinków 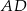 i
i 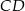 odpowiednio. Przedstawiono również okrąg, który jest styczny do dwóch boków kwadratu
odpowiednio. Przedstawiono również okrąg, który jest styczny do dwóch boków kwadratu 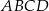 i przechodzi przez punkt
i przechodzi przez punkt 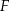 . Wykaż, że jeżeli
. Wykaż, że jeżeli 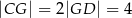 , to promień okręgu jest równy
, to promień okręgu jest równy 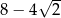 .
.
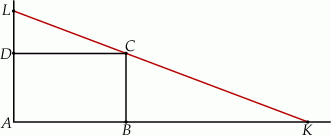
Przez wierzchołek 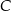 prostokąta
prostokąta 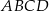 poprowadzono prostą, która przecięła proste
poprowadzono prostą, która przecięła proste 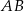 i
i 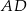 w punktach
w punktach 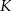 i
i 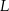 odpowiednio. Wykaż, że
odpowiednio. Wykaż, że 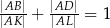 .
.
Uzasadnij, że jeżeli prostokąt  nie jest kwadratem, to punkty przecięcia dwusiecznych jego kątów wewnętrznych są wierzchołkami kwadratu.
nie jest kwadratem, to punkty przecięcia dwusiecznych jego kątów wewnętrznych są wierzchołkami kwadratu.

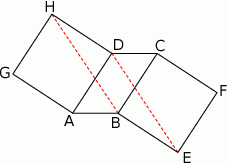
Na przeciwległych bokach równoległoboku 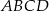 zbudowano kwadraty
zbudowano kwadraty 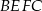 i
i 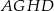 . Udowodnij, że proste
. Udowodnij, że proste 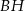 i
i 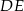 są równoległe.
są równoległe.
Podstawy trapezu mają długości 4 i 8. Kąty, jakie tworzą ramiona z dłuższą podstawą, mają miary 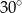 i
i 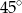 . Oblicz pole trapezu.
. Oblicz pole trapezu.
W trapezie, którego podstawy mają długości 10 cm i 4 cm, miary kątów przy dłuższej podstawie wynoszą 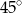 i
i 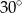 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
W trapezie, którego podstawy mają długości 12 cm i 6 cm, miary kątów przy dłuższej podstawie wynoszą 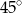 i
i 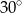 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.

