Na przekątnej 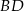 równoległoboku
równoległoboku 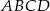 obrano dowolny punkt
obrano dowolny punkt 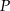 . Wykaż, że pola trójkątów
. Wykaż, że pola trójkątów 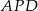 i
i 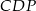 są równe.
są równe.
/Szkoła średnia/Geometria/Planimetria/Czworokąt
Na przekątnej 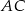 równoległoboku
równoległoboku 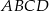 zaznaczono dowolny punkt
zaznaczono dowolny punkt 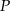 . Udowodnij, że pola trójkątów
. Udowodnij, że pola trójkątów 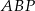 i
i 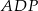 są równe.
są równe.
Dany jest czworokąt 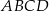 , w którym
, w którym 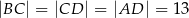 .
.
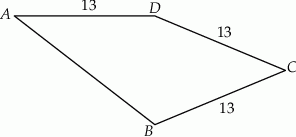
Przekątna 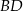 tego czworokąta ma długość 10 i jest prostopadła do boku
tego czworokąta ma długość 10 i jest prostopadła do boku 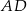 . Oblicz pole czworokąta
. Oblicz pole czworokąta 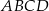 .
.
Oblicz pole rombu, którego jeden z kątów wewnętrznych wynosi 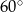 , a przekątna poprowadzona z wierzchołka tego kąta ma długość 20 cm.
, a przekątna poprowadzona z wierzchołka tego kąta ma długość 20 cm.
Pole trapezu jest równe 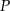 , a stosunek długości podstaw trapezu wynosi 2. Przekątne dzielą ten trapez na cztery trójkąty. Oblicz pole każdego z tych trójkątów.
, a stosunek długości podstaw trapezu wynosi 2. Przekątne dzielą ten trapez na cztery trójkąty. Oblicz pole każdego z tych trójkątów.
W trapezie 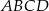 podstawy
podstawy 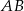 i
i 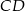 oraz ramię
oraz ramię 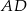 mają długości odpowiednio 15 cm, 12 cm i 6 cm. O ile centymetrów należy przedłużyć ramię
mają długości odpowiednio 15 cm, 12 cm i 6 cm. O ile centymetrów należy przedłużyć ramię 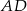 , by przecięło się z przedłużeniem ramienia
, by przecięło się z przedłużeniem ramienia 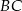 ?
?
Dany jest romb, którego kąt ostry ma miarę 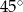 , a jego pole jest równe
, a jego pole jest równe 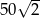 . Oblicz wysokość tego rombu.
. Oblicz wysokość tego rombu.
Dany jest romb, którego kąt ostry ma miarę 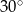 , a jego pole jest równe
, a jego pole jest równe 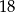 . Oblicz wysokość tego rombu.
. Oblicz wysokość tego rombu.
Oblicz wysokość trapezu o podstawach długości 18 i 14 oraz ramionach długości 3.
W równoległoboku 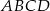 , w którym
, w którym 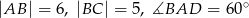 poprowadzono wysokości
poprowadzono wysokości 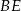 i
i 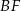 na boki
na boki 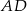 i
i 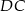 .
.
- Wykonaj odpowiedni rysunek i oblicz długości odcinków
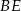 i
i 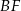 .
. - Oblicz pole trójkąta
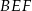 .
.
W trapezie równoramiennym, który nie jest równoległobokiem, ramię ma długość 7 cm, a przekątna 8 cm. Oblicz długości podstaw trapezu wiedząc, że odcinek łączący środki ramion trapezu ma długość 4 cm.
Na trapezie opisano okrąg o średnicy długości 25 cm. Dłuższa podstawa trapezu jest średnicą tego okręgu. Wiedząc, że przekątna tego trapezu ma długość 20 cm, oblicz pole tego trapezu.
Niech 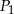 będzie prostokątem o bokach długości 3 i 8. Obok tego prostokąta rysujemy kolejne prostokąty
będzie prostokątem o bokach długości 3 i 8. Obok tego prostokąta rysujemy kolejne prostokąty 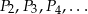 w ten sposób, że każdy z boków kolejnego prostokąta jest o 2 dłuższy od odpowiadających boków poprzedniego prostokąta.
w ten sposób, że każdy z boków kolejnego prostokąta jest o 2 dłuższy od odpowiadających boków poprzedniego prostokąta.
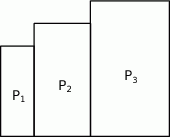
Wyznacz liczbę  , dla której obwód prostokąta
, dla której obwód prostokąta 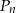 jest równy 246.
jest równy 246.
W trapezie równoramiennym długość krótszej podstawy wynosi 9 cm, przekątnej 17 cm a ramienia 10 cm. Oblicz jego pole.
Dany jest trapez opisany na okręgu, którego kąty przy jednej podstawie są ostre, oraz którego pole jest równe 168. Przekątne dzielą ten trapez na cztery trójkąty. Oblicz pole każdego z tych trójkątów jeżeli ramiona trapezu mają długości 13 i 15.
Dany jest prostokąt o bokach  i
i 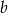 oraz prostokąt o bokach
oraz prostokąt o bokach  i
i 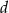 . Długość boku
. Długość boku  to 90% długości boku
to 90% długości boku  . Długość boku
. Długość boku 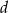 to 120% długości boku
to 120% długości boku 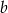 . Oblicz, ile procent pola prostokąta o bokach
. Oblicz, ile procent pola prostokąta o bokach  i
i 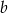 stanowi pole prostokąta o bokach
stanowi pole prostokąta o bokach  i
i 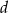 .
.
Dany jest prostokąt o bokach  i
i 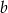 oraz prostokąt o bokach
oraz prostokąt o bokach  i
i 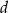 . Długość boku
. Długość boku  to 80% długości boku
to 80% długości boku  . Długość boku
. Długość boku 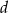 to 140% długości boku
to 140% długości boku 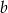 . Oblicz, ile procent pola prostokąta o bokach
. Oblicz, ile procent pola prostokąta o bokach  i
i 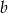 stanowi pole prostokąta o bokach
stanowi pole prostokąta o bokach  i
i 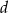 .
.
Punkt 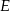 leży na ramieniu
leży na ramieniu 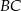 trapezu
trapezu 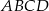 , w którym
, w którym 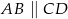 . Udowodnij, że
. Udowodnij, że 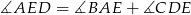 .
.
Dany jest romb 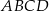 o boku długości 26, w którym przekątna
o boku długości 26, w którym przekątna 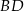 ma długość równą 20. Punkt
ma długość równą 20. Punkt 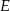 jest środkiem boku
jest środkiem boku 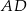 (zobacz rysunek).
(zobacz rysunek).
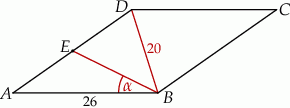
Oblicz sinus kąta  , jaki odcinek
, jaki odcinek 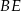 tworzy z bokiem
tworzy z bokiem 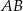 rombu
rombu 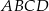 .
.
Trapez równoramienny 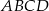 o ramieniu długości 6 wpisany jest w okrąg, przy czym dłuższa podstawa
o ramieniu długości 6 wpisany jest w okrąg, przy czym dłuższa podstawa 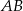 trapezu, o długości 12, jest średnicą tego okręgu. Przekątne
trapezu, o długości 12, jest średnicą tego okręgu. Przekątne 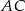 i
i 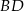 trapezu przecinają się w punkcie
trapezu przecinają się w punkcie 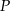 . Oblicz pole koła wpisanego w trójkąt
. Oblicz pole koła wpisanego w trójkąt 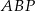 .
.
Trapez równoramienny 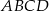 o ramieniu długości 7 wpisany jest w okrąg, przy czym dłuższa podstawa
o ramieniu długości 7 wpisany jest w okrąg, przy czym dłuższa podstawa 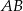 trapezu, o długości 14, jest średnicą tego okręgu. Przekątne
trapezu, o długości 14, jest średnicą tego okręgu. Przekątne 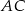 i
i 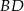 trapezu przecinają się w punkcie
trapezu przecinają się w punkcie 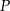 . Oblicz długość okręgu wpisanego w trójkąt
. Oblicz długość okręgu wpisanego w trójkąt 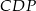 .
.
W romb, którego bok ma długość 5 cm, a kąt ostry ma miarę 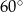 , wpisano okrąg. Oblicz pole czworokąta otrzymanego przez połączenie kolejnych punktów styczności tego okręgu z bokami rombu.
, wpisano okrąg. Oblicz pole czworokąta otrzymanego przez połączenie kolejnych punktów styczności tego okręgu z bokami rombu.
W romb o boku 8 i kącie ostrym 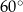 wpisano okrąg. Wyznacz pole prostokąta, którego wierzchołki leżą w punktach styczności okręgu z bokami rombu.
wpisano okrąg. Wyznacz pole prostokąta, którego wierzchołki leżą w punktach styczności okręgu z bokami rombu.
W równoległoboku 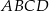 przekątna
przekątna 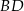 ma długość
ma długość 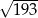 , a wysokość
, a wysokość 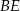 dzieli bok
dzieli bok 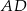 na odcinki o długościach
na odcinki o długościach 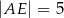 i
i 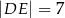 (zobacz rysunek).
(zobacz rysunek).
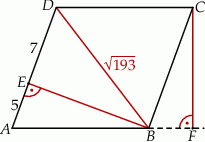
Oblicz długość wysokości 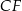 tego równoległoboku.
tego równoległoboku.
Podaj wymiary prostokąta, którego boki różnią się o 6 cm, a przekątna ma długość 30 cm.

