W trapez wpisano okrąg. Punkt styczności okręgu z dłuższą podstawą trapezu dzieli tę podstawę na odcinki długości 2,5 dm i 4 dm. Wysokość trapezu ma długość 4 dm. Oblicz obwód tego trapezu.
/Szkoła średnia/Geometria/Planimetria/Czworokąt
Z punktu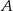 
leżącego na okręgu o promieniu 
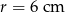i środku 
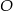poprowadzono dwie równej długości cięciwy 
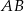i 
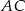tworzące kąt 
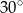. Oblicz pole czworokąta 
.
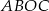W prostokącie połączono środki sąsiednich boków. Powstały w ten sposób romb ma obwód 40 cm i pole równe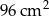 
. Oblicz długości boków prostokąta.
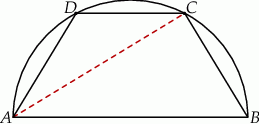
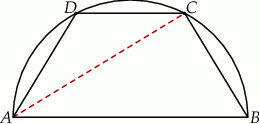
W półkole o promieniu 
wpisano trapez równoramienny o krótszej podstawie długości 
. Oblicz długość przekątnej trapezu.
Ukryj
Podobne zadania
W półkole o promieniu 
wpisano trapez równoramienny o przekątnej długości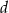 
. Oblicz długość krótszej podstawy trapezu.
W trójkąt równoramienny o ramieniu 10 i podstawie 12 wpisano prostokąt o stosunku boków 1:4 w ten sposób, ze krótszy bok jest zawarty w podstawie trójkąta. Oblicz długości boków prostokąta.
Kąty ostre trapezu opisanego na okręgu mają miary 
i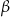 
, a pole tego trapezu jest równe 
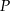. Oblicz długość promienia okręgu wpisanego w ten trapez.
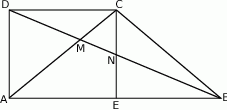
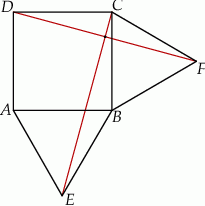
Punkt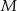 
jest punktem wspólnym przekątnych trapezu prostokątnego 
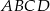. Punkt 
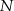jest punktem wspólnym przekątnej 
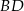i wysokości 
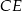opuszczonej na dłuższą podstawę 
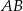. Wykaż, że 
.
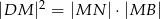Dany jest równoległobok 
, w którym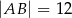 
, 
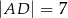oraz
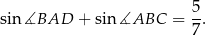
Oblicz pole równoległoboku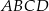 
.
Na zewnątrz kwadratu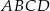 
na bokach 
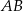i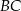 
zbudowano trójkąty równoboczne 
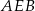i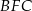 
. Uzasadnij, że proste 
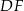i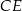 
są prostopadłe.
Wykaż, że punkt przecięcia przekątnych trapezu leży na prostej przechodzącej przez środki jego podstaw.
W trapezie równoramiennym krótsza podstawa i ramię mają taką samą długość. Przekątna trapezu tworzy z jednym z ramion kąt prosty. Oblicz miary kątów tego trapezu.
Niech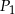 
będzie prostokątem o polu 
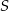i stosunku długości boków równym 3:2. Konstruujemy kolejno prostokąty 
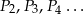podobne do prostokąta 
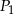takie, że dłuższy bok kolejnego prostokąta jest równy krótszemu bokowi poprzedniego prostokąta. Oblicz sumę pól prostokątów 
.
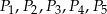