/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 1128583

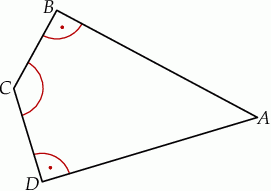
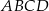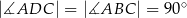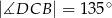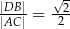W czworokącie wypukłym ABCD (zobacz rysunek poniżej) dane są kąty: |∡ADC | = |∡ABC | = 90∘ oraz |∡DCB | = 135∘ . Wykaż, że √- |DB-|= -2- |AC | 2 .

PIC

Wersja PDF

Rozwiązanie

Zauważmy, że na czworokącie ABCD można opisać okrąg.

PIC

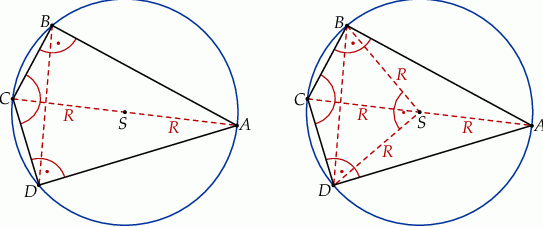
Dokładniej mówiąc, okrąg o średnicy 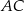AC przechodzi przez punkty 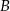B i D .

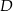Sposób I

Jeżeli więc oznaczymy 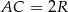AC = 2R to na mocy twierdzenia sinusów w trójkącie 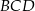BCD mamy

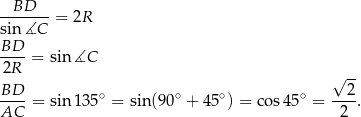
--BD--- sin ∡C = 2R BD ---- = sin∡C 2R √ -- BD ∘ ∘ ∘ ∘ 2 AC-- = sin1 35 = sin(90 + 45 ) = cos45 = -2-.

Sposób II

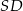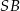Dorysujmy promienie SD i SB . Otrzymany trójkąt 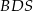BDS jest równoramienny oraz

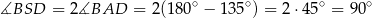
∘ ∘ ∘ ∘ ∡BSD = 2∡BAD = 2(18 0 − 135 ) = 2 ⋅45 = 9 0

(skorzystaliśmy z faktu, że suma miar przeciwległych kątów w czworokącie wpisanym w okrąg jest równa 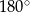180∘ ). W takim razie trójkąt 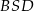BSD to równoramienny trójkąt prostokątny, czyli

√ -- √ -- √ -- 2 BD = SD 2 = R 2 = ----AC . 2
Wersja PDF