Zadanie nr 1271760
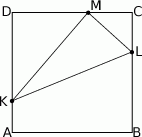
Na bokach 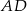 ,
, 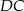 i
i 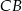 kwadratu
kwadratu 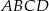 wybrano punkty
wybrano punkty 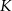 ,
, 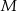 i
i 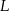 ten sposób, że
ten sposób, że 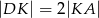 ,
, 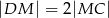 , oraz
, oraz 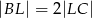 .
.
- Uzasadnij, że trójkąt
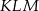 jest prostokątny.
jest prostokątny. - Oblicz tangensy kątów ostrych trójkąta
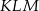 .
.
Rozwiązanie
-
Sposób I
Z podanych informacji wynika, że trójkąty
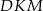 i
i 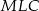 są równoramienne. W szczególności miary ich kątów ostrych wynoszą
są równoramienne. W szczególności miary ich kątów ostrych wynoszą 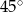 . Stąd
. Stąd 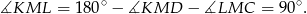
Sposób II
Na mocy twierdzenia Talesa prosta
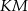 jest równoległa do przekątnej
jest równoległa do przekątnej 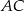 . Podobnie, prosta
. Podobnie, prosta 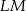 jest równoległa do przekątnej
jest równoległa do przekątnej 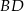 . Ponieważ przekątne kwadratu są prostopdałe, to prostopadłe są również proste
. Ponieważ przekątne kwadratu są prostopdałe, to prostopadłe są również proste 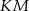 i
i 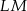 .
. - Oznaczmy bok kwadratu przez
 . Korzystając z twierdzenia Pitagorasa wyliczmy długości odcinków
. Korzystając z twierdzenia Pitagorasa wyliczmy długości odcinków 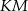 i
i  .
. 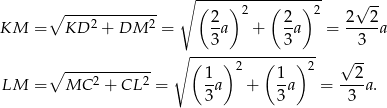
Stąd szukane tangensy wynoszą
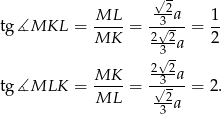
Odpowiedź: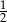 i 2
i 2

