/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 2464724

Dodaj do ulubionych
Dodaj do rozwiązanych

Dwa przeciwległe boki kwadratu wydłużono dwukrotnie, a każdy z dwóch pozostałych skrócono o 3 cm. Pole otrzymanego prostokąta jest o 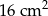1 6 cm 2 większe od pola kwadratu. Oblicz długości boków prostokąta.

Rozwiązanie

Oznaczmy przez a długość boku kwadratu.

PIC

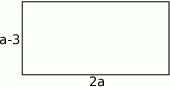
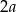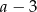Po opisanych zmianach otrzymamy prostokąt o bokach długości: 2a i a − 3 . Z podanego pola mamy więc równanie

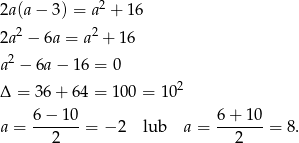
2a (a− 3) = a2 + 16 2 2 2a − 6a = a + 16 a 2 − 6a − 1 6 = 0 2 Δ = 36 + 6 4 = 100 = 1 0 6 − 10 6 + 10 a = -------= − 2 lub a = -------= 8. 2 2

Ujemne rozwiązanie odrzucamy i mamy 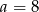a = 8 , czyli prostokąt ma boki długości 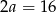2a = 16 i a − 3 = 5 .  
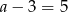Odpowiedź: 16 cm i 5 cm

Wersja PDF