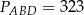Zadanie nr 2501194
Przekątne trapezu równoramiennego 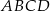 przecinają się w punkcie
przecinają się w punkcie 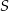 . Przekątna
. Przekątna 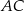 tworzy z dłuższą podstawą
tworzy z dłuższą podstawą 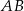 kąt
kąt  i z ramieniem
i z ramieniem 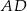 kąt
kąt 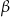 takie, że
takie, że 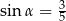 i
i 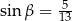 . Pole trapezu
. Pole trapezu 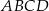 jest równe 448. Oblicz pole trójkąta
jest równe 448. Oblicz pole trójkąta 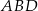 .
.
Rozwiązanie
Zaczynamy naturalnie od rysunku.
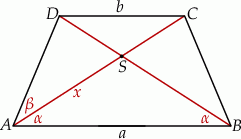
Trójkąty 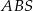 i
i 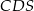 mają równe kąty, więc są podobne. Spróbujmy, korzystając z podanych sinusów, obliczyć skalę
mają równe kąty, więc są podobne. Spróbujmy, korzystając z podanych sinusów, obliczyć skalę 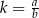 ich podobieństwa. Zrobimy to stosując twierdzenie sinusów w trójkącie
ich podobieństwa. Zrobimy to stosując twierdzenie sinusów w trójkącie 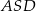 , ale najpierw zauważmy, że
, ale najpierw zauważmy, że
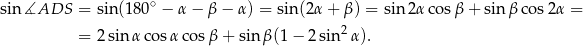
Do dokończenia tego rachunku potrzebujemy jeszcze
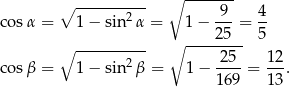
Mamy zatem
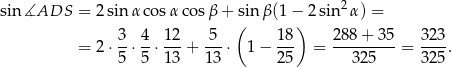
Stosujemy teraz twierdzenie sinusów w trójkącie 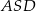 .
.
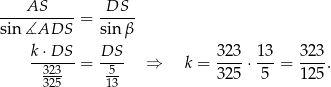
To pozwala nam obliczyć pole trójkąta  .
.
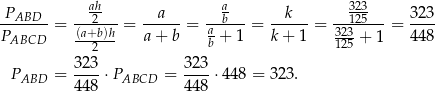
Odpowiedź: