Zadanie nr 2575707
W trapez 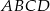 , gdzie
, gdzie 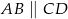 i
i 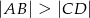 , wpisano okrąg (patrz rysunek).
, wpisano okrąg (patrz rysunek).
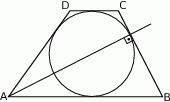
Dwusieczna kąta ostrego przy wierzchołku 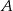 jest prostopadła do ramienia
jest prostopadła do ramienia 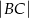 .
.
- Wykaż, że dwusieczna kąta przy wierzchołku
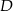 jest równoległa do ramienia
jest równoległa do ramienia 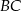 .
. - Oblicz
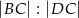 .
.
Rozwiązanie
Niech 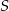 będzie środkiem okręgu wpisanego w trapez.
będzie środkiem okręgu wpisanego w trapez.
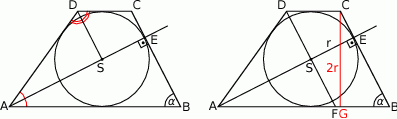
- Dorysujmy odcinek
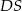 i oznaczmy
i oznaczmy 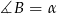 . Z trójkąta prostokątnego
. Z trójkąta prostokątnego 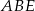 mamy
mamy 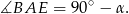
Ponieważ promień
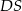 jest zawarty w dwusiecznej kąta
jest zawarty w dwusiecznej kąta 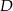 mamy
mamy 
Zatem odcinki
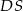 i
i 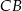 tworzą takie same kąty z równoległymi prostymi
tworzą takie same kąty z równoległymi prostymi 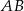 i
i 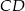 . Są więc równoległe.
. Są więc równoległe. - Przedłużmy promień
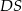 do jego przecięcia
do jego przecięcia 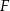 z podstawą
z podstawą 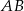 . Z poprzedniego podpunkty wiemy, że czworokąt
. Z poprzedniego podpunkty wiemy, że czworokąt 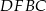 jest równoległobokiem. Znamy ponadto długości dwóch jego wysokości:
jest równoległobokiem. Znamy ponadto długości dwóch jego wysokości: 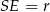 i
i 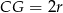 , gdzie
, gdzie  jest długością promienia okręgu wpisanego. Licząc pole równoległoboku
jest długością promienia okręgu wpisanego. Licząc pole równoległoboku 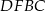 na dwa sposoby otrzymujemy
na dwa sposoby otrzymujemy 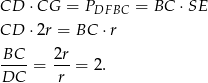
Odpowiedź: 2

