/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 2688091

Dodaj do ulubionych
Dodaj do rozwiązanych

Na kole opisany jest romb. Stosunek pola koła do pola powierzchni rombu wynosi 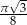√- π--3 8 . Wyznacz miarę kąta ostrego rombu.

Rozwiązanie

Zacznijmy od rysunku.

PIC

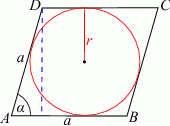
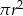Przyjmijmy oznaczenia jak na rysunku, tzn. r –promień koła wpisanego, a –długość boku, α –kąt ostry w rombie. Przy takich oznaczeniach, pole koła wynosi πr 2 , a pole rombu 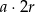a ⋅2r . Z danych zadania wiemy ile wynosi stosunek tych pól, co daje nam równanie:

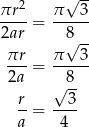
-- πr 2 π √ 3 ----= ----- 2ar 8√ -- πr- π---3 2a = 8 √ -- r-= --3- a 4

Z drugiej strony, 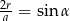2ra = sin α , skąd 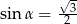√3 sin α = -2- , czyli α = 60∘ .  
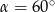Odpowiedź: 60∘

Wersja PDF