/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 2833903

Dodaj do ulubionych
Dodaj do rozwiązanych

W romb o boku długości 10 cm i wysokości 8 cm wpisano okrąg o1 .

  • Oblicz w jakiej odległości od środka boku znajduje się punkt styczności okręgu z tym bokiem.
  • Uzasadnij, że przez środki boków tego rombu można poprowadzić okrąg o2 i wyznacz długość promienia tego okręgu.
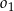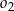  • Korzystając z wyliczonych wielkości narysuj ten romb wraz z okręgami o1 i o2 w skali 1:2.

Rozwiązanie

Zaczynamy od szkicowego rysunku.

PIC

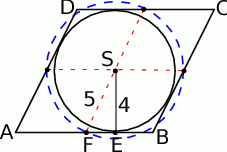
  • Środek okręgu wpisanego w romb to punkt przecięcia się przekątnych 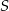S . Przez ten punkt przechodzą również odcinki łączące środki przeciwległych boków rombu. Punkt 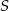S dzieli każdy z tych odcinków na połowę, więc z trójkąta 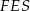FES mamy
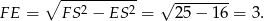
    ∘ ----------- √ -------- F E = FS 2 − ES 2 = 2 5− 1 6 = 3.

     
    Odpowiedź: 3 cm

  • Wystarczy zauważyć, że wszystkie środki boków są odległe od punktu 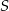S o 5 cm, zatem okrąg o takim promieniu i środku 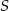S przechodzi przez wszystkie środki boków.  
    Odpowiedź: promień: 5 cm
  • Rysujemy najpierw okrąg o promieniu 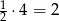12 ⋅4 = 2 , potem styczną do tego okręgu. Na tej stycznej odmierzamy od punktu styczności odcinki długości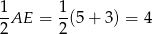
    1 1 --AE = --(5+ 3) = 4 2 2

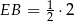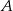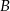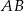    i 1 EB = 2 ⋅2 . Daje to nam punkty A i B . Potem z tych punktów prowadzimy styczne i znajdujemy jej punkty wspólne z styczną równoległą do AB .

Wersja PDF