Zadanie nr 2895060
Dany jest równoległobok, którego obwód jest równy 50 cm. Stosunek długości jego wysokości wynosi 2:3, a stosunek miar jego kątów wewnętrznych jest równy 1:2. Oblicz długości boków i wysokości tego równoległoboku.
Rozwiązanie
Suma dwóch różnych kątów równoległoboku jest równa 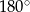 , więc jeżeli ich stosunek wynosi 1:2 to są one równe
, więc jeżeli ich stosunek wynosi 1:2 to są one równe
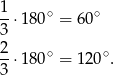
Naszkicujmy teraz sobie ten równoległobok.
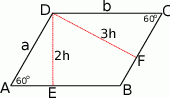
Skoro stosunek długości wysokości równoległoboku jest równy 2:3, możemy oznaczyć ich długości przez 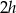 i
i 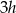 . Z trójkątów
. Z trójkątów 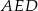 i
i 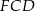 mamy
mamy
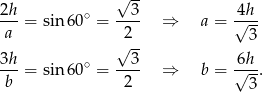
Teraz korzystamy z podanego obwodu
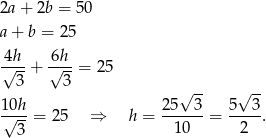
Zatem wysokości mają długości
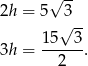
Długości boków są równe
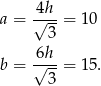
Odpowiedź: Wysokości: 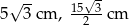 , boki: 10 cm, 15 cm
, boki: 10 cm, 15 cm

