/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 3044730

Dodaj do ulubionych
Dodaj do rozwiązanych

Ramiona trapezu opisanego na okręgu mają długości 3 cm i 5 cm. Odcinek łączący środki ramion dzieli trapez na dwie figury, których stosunek pól wynosi 5:11. Oblicz długości podstaw trapezu.

Rozwiązanie

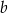Zacznijmy od rysunku oraz obserwacji, że odcinek łączący środki ramion trapezu o podstawach a i b ma długość 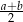a+2b- – uzasadnienie łatwo odczytać z prawego rysunku.

PIC

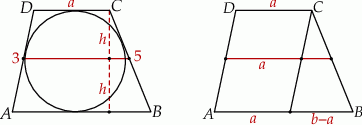
Ponieważ w trapez można wpisać okrąg, sumy przeciwległych boków są sobie równe. Jeżeli więc oznaczymy 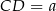CD = a , to mamy

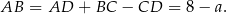
AB = AD + BC − CD = 8 − a.

W szczególności odcinek łączący środki ramion trapezu ma długość

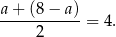
a-+-(8-−-a) = 4 . 2

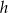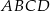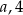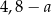Trapezy, na które został podzielony trapez tym odcinkiem mają taką samą wysokość h (połowa wysokości trapezu ABCD ) oraz podstawy a,4 i 4,8 − a odpowiednio. Zatem stosunek ich pól wynosi

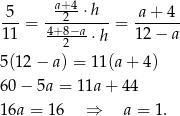
5 a+4-⋅h a+ 4 ---= 4+28−a----= ------- 11 --2---⋅h 12 − a 5(12− a) = 11(a + 4) 60− 5a = 11a + 44 16a = 16 ⇒ a = 1.

Stąd 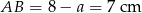AB = 8 − a = 7 cm .  
Odpowiedź: 1 cm i 7 cm

Wersja PDF