/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 3168794

Dodaj do ulubionych
Dodaj do rozwiązanych

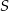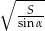Pole trapezu równoramiennego opisanego na okręgu jest równe S , a kąt ostry przy podstawie ma miarę α . Wykaż, że ramię tego trapezu ma długość ∘ ---- -S-- sinα .

Rozwiązanie

Zaczynamy od rysunku.

PIC

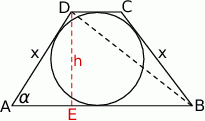
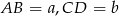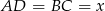Jeżeli oznaczymy AB = a,CD = b i AD = BC = x , to ponieważ czworokąt 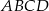ABCD jest opisany na okręgu, mamy

a + b = 2x.

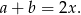
Sposób I

Obliczamy pole trapezu 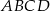ABCD jako sumę pól trójkątów 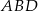ABD i BDC .

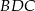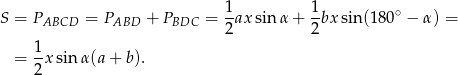
S = P = P + P = 1-ax sin α + 1-bxsin(18 0∘ − α) = ABCD ABD BDC 2 2 1 = --xsin α(a + b). 2

Korzystamy teraz z tego, że 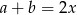a + b = 2x

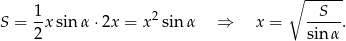
∘ ------ S = 1x sinα ⋅2x = x2sin α ⇒ x = --S--. 2 sin α

Sposób II

Jeżeli oznaczymy przez 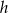h wysokość 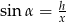h sin α = x trapezu i 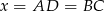x = AD = BC , to i mamy

a + b 2x S = ------⋅h = ---⋅x sin α = x 2sinα . 2 2 ∘ ------ 2 --S-- --S-- x = sin α ⇒ x = sin α.
Wersja PDF