/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 3220335

Dodaj do ulubionych
Dodaj do rozwiązanych

W prostokącie 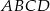ABCD , w którym 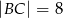|BC | = 8 połączono wierzchołek 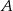A z punktem 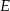E leżącym na boku 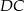DC . Odcinek ten przeciął przekątną 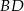BD w punkcie F .

PIC

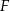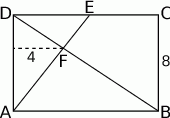
Wiedząc, że odległość punktu 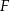F od boku 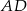AD jest równa 4, oraz że 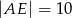|AE | = 10 oblicz długość boku 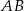AB prostokąta.

Rozwiązanie

Korzystając z twierdzenia Pitagorasa w trójkącie 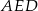AED mamy

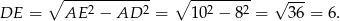
∘ ---2------2- ∘ --2----2- √ --- DE = AE − AD = 10 − 8 = 36 = 6.

To pozwala nam wyliczyć stosunek w jakim punkt 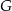G dzieli bok AD .

PIC

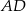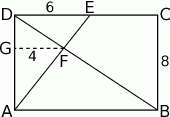
Na mocy twierdzenia Talesa mamy

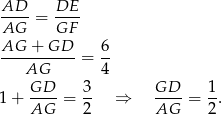
AD-- = DE-- AG GF AG--+-GD--- 6- AG = 4 GD 3 GD 1 1+ ----= -- ⇒ ----= --. AG 2 AG 2

Teraz bez trudu wyliczamy długość odcinka 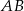AB . Ponownie stosujemy twierdzenie Talesa.

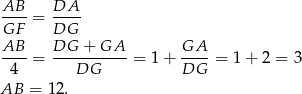
AB DA ----= ---- GF DG AB-- DG--+-GA--- GA-- 4 = DG = 1 + DG = 1 + 2 = 3 AB = 12.

 
Odpowiedź: AB = 12

Wersja PDF