/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 4308753

Dodaj do ulubionych
Dodaj do rozwiązanych

Długości boków równoległoboku są równe 13 i 21, a jego pole wynosi 252. Oblicz długości przekątnych tego równoległoboku.

Rozwiązanie

Sposób I

Zaczynamy od rysunku.

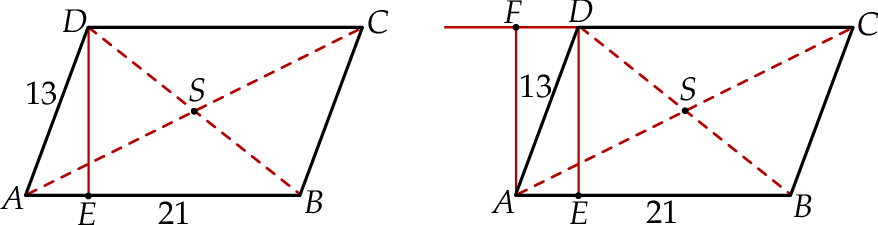
ZINFO-FIGURE

Ponieważ znamy długości boków oraz pole równoległoboku, możemy łatwo obliczyć długość jego wysokości.

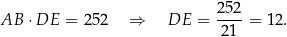
252 AB ⋅DE = 252 ⇒ DE = ----= 12. 21

Zajmijmy się teraz przekątną 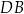DB . Można ją obliczyć z trójkąta prostokątnego 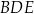BDE , ale najpierw musimy obliczyć długość odcinka 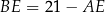BE = 21 − AE . Liczymy (z trójkąta AED )

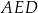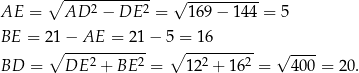
∘ ------------ √ ---------- AE = AD 2 − DE 2 = 169 − 14 4 = 5 BE = 2 1− AE = 21 − 5 = 1 6 ∘ ------------ ∘ ---------- √ ---- BD = DE 2 + BE 2 = 122 + 162 = 40 0 = 20.

Podobnie obliczamy długość drugiej przekątnej. Tym razem patrzymy na trójkąt 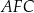AF C , gdzie 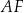AF jest wysokością opuszczoną na bok 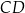CD z wierzchołka A .

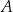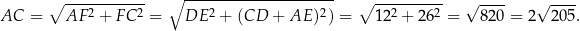
∘ ----------- ∘ --------------------- ∘ ---------- √ ---- √ ---- AC = AF 2 + FC 2 = DE 2 + (CD + AE )2) = 1 22 + 2 62 = 820 = 2 205.

Sposób II

Tym razem skorzystamy z twierdzenia cosinusów.

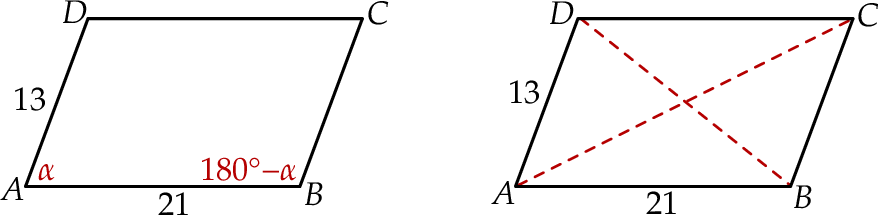
ZINFO-FIGURE

Oznaczmy tak jak na obrazku 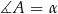∡A = α i przyjmijmy 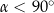∘ α < 90 (wtedy 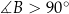∘ ∡B > 90 ). Ze wzoru na pole równoległoboku z sinusem mamy

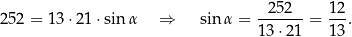
252 = 13 ⋅21 ⋅sinα ⇒ sin α = --252--= 12-. 13 ⋅21 13

Zatem

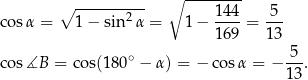
---------- ∘ -------- ∘ 2 144- 5-- cos α = 1 − sin α = 1 − 169 = 13 5 cos ∡B = cos(180 ∘ − α ) = − cos α = −---. 13

Piszemy teraz twierdzenie cosinusów w trójkącie 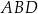ABD .

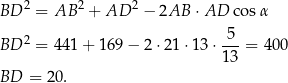
2 2 2 BD = AB + AD − 2AB ⋅AD co sα 2 5-- BD = 441+ 169 − 2 ⋅21⋅ 13⋅ 13 = 4 00 BD = 20.

Teraz piszemy twierdzenie cosinusów w trójkącie 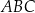ABC .

2 2 2 AC = AB + BC − 2AB ⋅ BC cos ∡B 2 5-- AC = 441+ 169 + 2 ⋅21 ⋅13⋅ 13 = 8 20 √ ---- √ ---- AC = 820 = 2 2 05.

 
Odpowiedź: √ ---- 20, 2 205

Wersja PDF