/Szkoła średnia/Zadania maturalne/Matura 2013/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 16 marca 2013 Czas pracy: 170 minut
Zadania zamknięte
Liczba 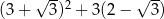 jest równa
jest równa
A) 18 B) 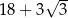 C)
C) 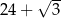 D) 24
D) 24
Liczbą odwrotną do liczby 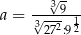 jest
jest
A) 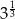 B)
B) 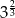 C)
C) 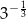 D)
D) 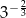
Jeżeli 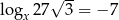 to liczba
to liczba  jest równa
jest równa
A) 3 B) 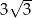 C)
C) 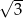 D)
D) 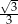
Badając pewien roztwór stwierdzono, że zawiera on 0,05 g chloru, co stanowi 0,02% masy roztworu. Jaka była masa roztworu?
A) 2,5 kg B) 250 g C) 25 g D) 2,5 g
Pole rombu o kącie ostrym 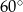 jest równe
jest równe 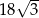 . Bok tego rombu ma długość
. Bok tego rombu ma długość
A) 9 B) 3 C) 6 D) 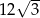
Wskaż nierówność, która opisuje przedział zaznaczony na osi liczbowej:
![]()
A) 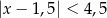 B)
B) 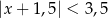 C)
C) 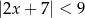 D)
D) 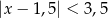
Miejscami zerowymi funkcji kwadratowej 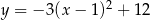 są
są
A) 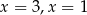 B)
B) 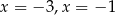 C)
C) 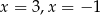 D)
D) 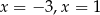
W trójkącie stosunek miar kątów jest równy 3:4:5. Zatem najmniejszy kąt tego trójkąta ma miarę
A) 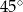 B)
B) 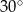 C)
C) 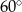 D)
D) 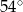
Punkty 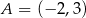 i
i 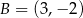 są wierzchołkami sześciokąta foremnego
są wierzchołkami sześciokąta foremnego 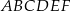 . Obwód tego sześciokąta jest równy
. Obwód tego sześciokąta jest równy
A) 50 B) 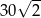 C) 300 D)
C) 300 D) 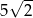
Wielomian 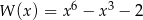 jest równy iloczynowi
jest równy iloczynowi
A) 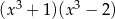 B)
B) 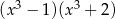 C)
C) 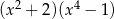 D)
D) 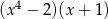
Pięciokąt 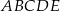 jest foremny. Wskaż trójkąt przystający do trójkąta
jest foremny. Wskaż trójkąt przystający do trójkąta 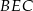
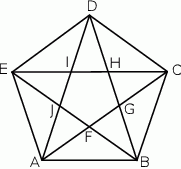
A) 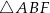 B)
B) 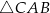 C)
C) 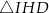 D)
D) 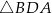
W trójkącie prostokątnym 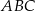 odcinek
odcinek 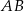 jest przeciwprostokątną i
jest przeciwprostokątną i 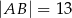 oraz
oraz 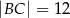 . Wówczas tangens kąta
. Wówczas tangens kąta 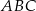 jest równy
jest równy
A) 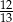 B)
B) 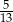 C)
C) 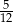 D)
D) 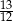
Równanie 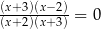 ma
ma
A) dokładnie jedno rozwiązanie
B) dokładnie dwa rozwiązania
C) dokładnie trzy rozwiązania
D) dokładnie cztery rozwiązania
W ciągu arytmetycznym 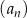 wyraz
wyraz 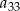 jest dwa razy większy od wyrazu
jest dwa razy większy od wyrazu 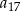 oraz
oraz 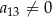 . Wtedy iloraz
. Wtedy iloraz 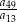 jest równy
jest równy
A) 1 B) 2 C) 3 D) 4
Pole kwadratu wpisanego w okrąg o średnicy 10 jest równe
A) 100 B) 75 C) 50 D) 25
Ciąg 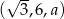 jest geometryczny. Wówczas
jest geometryczny. Wówczas
A) 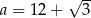 B)
B) 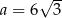 C)
C) 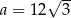 D)
D) 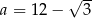
Kąt wpisany w okrąg o promieniu 5, który jest oparty na łuku długości 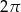 ma miarę
ma miarę
A) 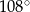 B)
B) 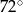 C)
C) 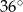 D)
D) 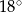
Na którym rysunku przedstawiono wykres funkcji liniowej 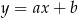 takiej, że
takiej, że 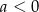 i
i 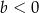 ?
?
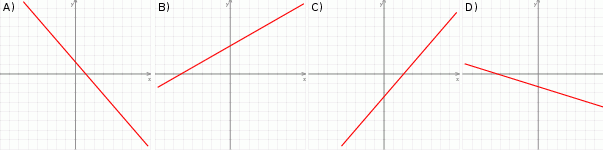
Pole powierzchni całkowitej sześcianu jest równe 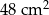 . Długość przekątnej podstawy tego sześcianu jest równa
. Długość przekątnej podstawy tego sześcianu jest równa
A) 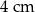 B)
B) 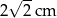 C)
C) 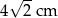 D)
D) 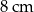
Wykres funkcji 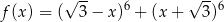 przecina oś
przecina oś 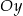 w punkcie
w punkcie
A) 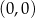 B)
B) 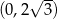 C)
C) 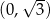 D)
D) 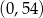
Wybieramy liczbę  ze zbioru
ze zbioru 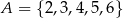 oraz liczbę
oraz liczbę 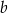 ze zbioru
ze zbioru 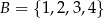 . Ile jest takich par
. Ile jest takich par 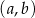 , że iloczyn
, że iloczyn 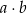 jest liczbą parzystą?
jest liczbą parzystą?
A) 11 B) 16 C) 20 D) 9
Trójkąt prostokątny o przyprostokątnych 4 i 6 obracamy wokół krótszej przyprostokątnej. Objętość powstałego stożka jest równa:
A) 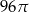 B)
B) 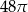 C)
C) 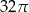 D)
D) 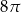
Na okręgu o równaniu 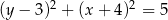 leży punkt
leży punkt
A) 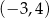 B)
B) 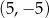 C)
C) 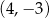 D)
D) 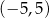
Jeżeli 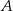 i
i 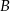 są zdarzeniami losowymi,
są zdarzeniami losowymi, 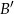 jest zdarzeniem przeciwnym do
jest zdarzeniem przeciwnym do 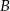 ,
, 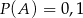 ,
, 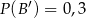 oraz
oraz 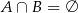 , to
, to 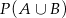 jest równe
jest równe
A) 0,4 B) 0,2 C) 0,8 D) 0,9
Zadania otwarte
Wyznacz wszystkie liczby pierwsze spełniające nierówność 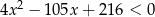 .
.
Rozwiąż równanie 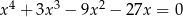 .
.
Uzasadnij, że jeśli liczby rzeczywiste 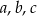 spełniają nierówności:
spełniają nierówności: 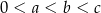 , to
, to
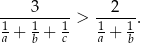
Pierwszy wyraz ciągu arytmetycznego jest równy 4, piąty wyraz tego ciągu jest równy 16. Oblicz sumę siedmiu początkowych wyrazów tego ciągu.
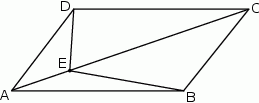
Na przekątnej 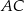 równoległoboku
równoległoboku 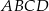 wybrano punkt
wybrano punkt 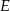 (zobacz rysunek). Uzasadnij, że trójkąty
(zobacz rysunek). Uzasadnij, że trójkąty 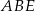 i
i 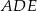 mają równe pola.
mają równe pola.
Dany jest kwadrat 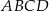 o polu 10 i wierzchołku
o polu 10 i wierzchołku 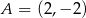 . Przekątna
. Przekątna 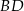 tego kwadratu ma równanie
tego kwadratu ma równanie 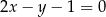 . Oblicz współrzędne pozostałych wierzchołków kwadratu.
. Oblicz współrzędne pozostałych wierzchołków kwadratu.
Firma odzieżowa otrzymała zamówienie na wykonanie 600 kurtek. Aby zrealizować zamówienie firma postanowiła wykonywać dziennie tę samą liczbę kurtek. Po wykonaniu 60% zamówienia usprawniono produkcję tak, że dzienna produkcja wzrosła o 6 kurtek, zaś zamówienie zrealizowano o 2 dni wcześniej w stosunku do pierwotnego planu. W ciągu ilu dni zrealizowano zamówienie?
Dany jest graniastosłup prawidłowy trójkątny 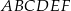 o podstawach
o podstawach 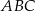 i
i 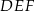 i krawędziach bocznych
i krawędziach bocznych 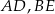 i
i 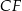 (zobacz rysunek). Punkt
(zobacz rysunek). Punkt 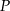 jest środkiem krawędzi
jest środkiem krawędzi 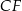 . Długość krawędzi podstawy
. Długość krawędzi podstawy 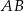 jest równa 12, a pole trójkąta
jest równa 12, a pole trójkąta 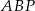 jest równe
jest równe 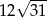 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.