/Gimnazjum/Egzamin gimnazjalny/Egzamin 2014/Egzamin
Egzamin Gimnazjalny
z Matematyki 24 kwietnia 2014 Czas pracy: 90 minut
Informacja do zadań 1 i 2
Promocja w zakładzie optycznym jest związana z wiekiem klienta i polega na tym, że klient otrzymuje tyle procent zniżki, ile ma lat.
Cena okularów bez promocji wynosi 240 zł. Ile zapłaci za te okulary klient, który ma 35 lat? Wybierz odpowiedź spośród podanych.
A) 84 zł B) 132 zł C) 156 zł D) 205 zł
Okulary bez promocji kosztują 450 zł, a klient zgodnie z obowiązującą promocją może je kupić za 288 zł. Ile lat ma ten klient? Wybierz odpowiedź spośród podanych.
A) 64 B) 56 C) 44 D) 36
Sześć maszyn produkuje pewną partię jednakowych butelek z tworzywa sztucznego przez 4 godziny. Każda z maszyn pracuje z taką samą stałą wydajnością.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Przez 8 godzin taką samą partię butelek wykonają 3 takie maszyny. | P | F |
| Połowę partii takich butelek 6 maszyn wykona przez 2 godziny. | P | F |
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Liczbą większą od 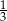 jest
jest
A) 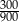 B)
B) 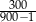 C)
C) 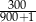 D)
D) 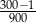
Dane są liczby: 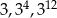 .
.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Iloczyn tych liczb jest równy
A) 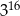 B)
B) 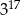 C)
C) 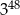 D)
D) 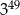
W zawodach sportowych każdy zawodnik miał pokonać trasę składającą się z trzech części. Pierwszą część trasy zawodnik przejechał na rowerze, drugą część – prowadzącą przez jezioro – przepłynął, a trzecią – przebiegł. Na rysunku przedstawiono schemat tej trasy.
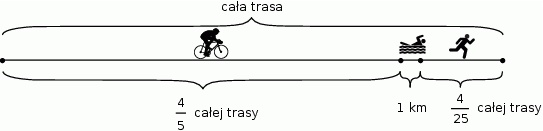
Na podstawie informacji wybierz zdanie prawdziwe.
A) Cała trasa miała długość 50 km.
B) Zawodnik przebiegł 8 km.
C) Odległość, którą zawodnik przebiegł, była o 4 km większa od odległości, którą przepłynął.
D) Odległość, którą zawodnik przejechał na rowerze, była 5 razy większa od odległości, którą przebiegł.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Liczba 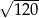 znajduje się na osi liczbowej między
znajduje się na osi liczbowej między
A) 10 i 11 B) 11 i 12 C) 12 i 20 D) 30 i 40
Rozwinięcie dziesiętne ułamka 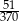 jest równe 0,1(378).
jest równe 0,1(378).
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Na pięćdziesiątym miejscu po przecinku tego rozwinięcia znajduje się cyfra
A) 1 B) 3 C) 7 D) 8
Informacja do zadań 9 i 10
Na rysunkach przedstawiono kształt i sposób układania płytek oraz niektóre wymiary w centymetrach.
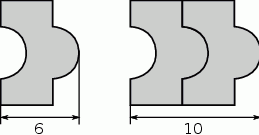
Ułożono wzór z 5 płytek, jak na rysunku.
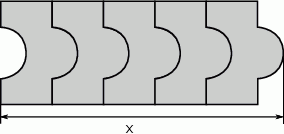
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Odcinek  ma długość
ma długość
A) 20 cm B) 22 cm C) 26 cm D) 30 cm
Które wyrażenie algebraiczne opisuje długość analogicznego do  odcinka dla wzoru złożonego z
odcinka dla wzoru złożonego z  płytek? Wybierz odpowiedź spośród podanych.
płytek? Wybierz odpowiedź spośród podanych.
A) 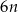 B)
B) 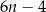 C)
C) 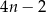 D)
D) 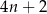
Prędkość średnia piechura na trasie 10 km wyniosła 5 km/h, a prędkość średnia rowerzysty na tej samej trasie była równa 20 km/h. O ile minut więcej zajęło pokonanie tej trasy piechurowi niż rowerzyście? Wybierz odpowiedź spośród podanych.
A) 30 minut B) 60 minut C) 90 minut D) 120 minut
Piechur szedł z punktu 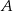 do punktu
do punktu 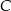 ze stałą prędkością. Część trasy przeszedł wzdłuż prostej, a część – po łuku okręgu o środku w punkcie
ze stałą prędkością. Część trasy przeszedł wzdłuż prostej, a część – po łuku okręgu o środku w punkcie 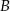 (patrz rysunek).
(patrz rysunek).
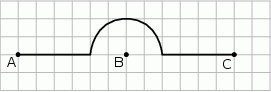
Na którym z poniższych wykresów zilustrowano, jak zmieniała się odległość piechura od punktu B? Wybierz odpowiedź spośród podanych.
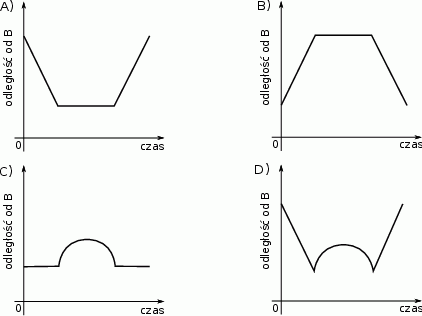
W prostokątnym układzie współrzędnych przedstawiono wykres funkcji.
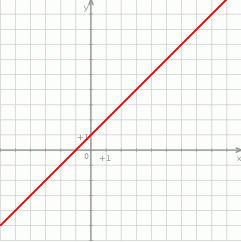
Które z poniższych zdań jest fałszywe? Wybierz odpowiedź spośród podanych.
A) Dla argumentu 2 wartość funkcji jest równa 3.
B) Funkcja przyjmuje wartość 0 dla argumentu 1.
C) Wartość funkcji jest równa 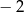 dla argumentu
dla argumentu 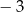 .
.
D) Dla argumentów większych od 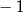 wartości funkcji są dodatnie.
wartości funkcji są dodatnie.
Rzucamy jeden raz sześcienną kostką do gry. Oznaczmy przez 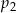 prawdopodobieństwo wyrzucenia liczby podzielnej przez 2, a przez
prawdopodobieństwo wyrzucenia liczby podzielnej przez 2, a przez 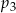 – prawdopodobieństwo wyrzucenia liczby podzielnej przez 3.
– prawdopodobieństwo wyrzucenia liczby podzielnej przez 3.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba 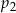 jest mniejsza od liczby jest mniejsza od liczby 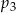 . . | P | F |
Liczby 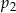 i i 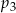 są mniejsze od są mniejsze od 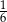 | P | F |
Ola codziennie, przez tydzień, odczytywała o 7 rano temperaturę powietrza. Oto podane (w 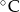 ) wyniki jej pomiarów:
) wyniki jej pomiarów: 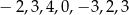 .
.

Wybierz odpowiedź, w której podano poprawne wartości średniej arytmetycznej, mediany i amplitudy (różnica między wartością najwyższą i wartością najniższą) zanotowanych temperatur.
Na rysunku przedstawiono prostokąt, którego wymiary są opisane za pomocą wyrażeń.
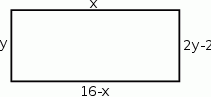
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jeden z boków prostokąta ma długość 8. | P | F |
| Obwód prostokąta jest równy 20. | P | F |
Szymon wykonał szkielet prostopadłościanu. Układał i sklejał ze sobą kolejno drewniane klocki sześcienne o krawędzi 4 cm wzdłuż każdej krawędzi prostopadłościennego pudełka o wymiarach: 36 cm, 28 cm, 20 cm. Na rysunku przedstawiono część wykonanego szkieletu.
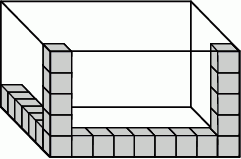
Ile klocków łącznie zużył Szymon na wykonanie całego szkieletu? Wybierz odpowiedź spośród podanych.
A) 84 B) 76 C) 68 D) 60
Na rysunku przedstawiono graniastosłup prosty i jego wymiary.
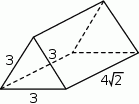
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Objętość tego graniastosłupa jest równa
A) 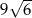 B)
B) 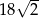 C)
C) 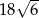 D)
D) 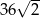
Maciek rysuje siatkę ostrosłupa prawidłowego, którego podstawą jest kwadrat o środku w punkcie 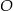 i boku długości 8.
i boku długości 8.
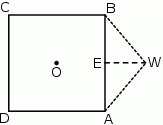
Czy trójkąt 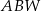 o bokach długości odpowiednio: 8, 5, 5 może być ścianą boczną takiego ostrosłupa? Wybierz odpowiedź T lub N i jej uzasadnienie spośród zdań A–C.
o bokach długości odpowiednio: 8, 5, 5 może być ścianą boczną takiego ostrosłupa? Wybierz odpowiedź T lub N i jej uzasadnienie spośród zdań A–C.
| Tak | Nie |
| ponieważ | |
| A) | trójkąt 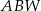 jest równoramienny. jest równoramienny. |
| B) | odległość 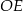 jest mniejsza niż wysokość jest mniejsza niż wysokość 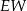 trójkąta trójkąta 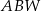 . . |
| C) | odległość 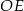 jest większa niż wysokość jest większa niż wysokość 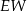 trójkąta trójkąta 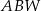 . . |
Dane są kula o środku w punkcie 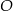 i promieniu
i promieniu  oraz walec o promieniu podstawy
oraz walec o promieniu podstawy  i wysokości
i wysokości  .
.
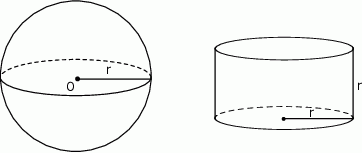
Na podstawie informacji wybierz zdanie prawdziwe.
A) Objętość kuli jest równa objętości walca.
B) Objętość kuli jest 2 razy większa od objętości walca.
C) Objętość walca stanowi  objętości kuli.
objętości kuli.
D) Objętość walca jest 3 razy mniejsza od objętości kuli.
Cena godziny korzystania z basenu wynosi 12 zł. Można jednak kupić miesięczną kartę rabatową za 50 złotych, upoważniającą do obniżki cen, i wtedy za pierwsze 10 godzin pływania płaci się 8 złotych za godzinę, a za każdą następną godzinę – 9 złotych. Wojtek kupił kartę rabatową i korzystał z basenu przez 16 godzin. Czy zakup karty był dla Wojtka opłacalny? Zapisz obliczenia.
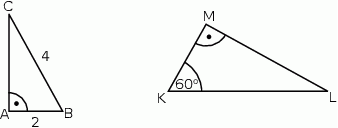
Uzasadnij, że trójkąty prostokątne 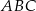 i
i 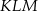 przedstawione na rysunku są podobne.
przedstawione na rysunku są podobne.
Z sześcianu zbudowanego z 64 małych sześcianów o krawędzi 1 cm usunięto z każdego narożnika po jednym małym sześcianie (patrz rysunek). Oblicz pole powierzchni powstałej bryły i porównaj je z polem powierzchni dużego sześcianu. Zapisz obliczenia.