Wyznacz największą wartość funkcji 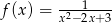 .
.
/Szkoła średnia/Funkcje
Reszta z dzielenia wielomianu 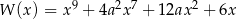 przez dwumian
przez dwumian 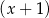 jest równa 2. Oblicz resztę z dzielenia wielomianu
jest równa 2. Oblicz resztę z dzielenia wielomianu 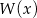 przez dwumian
przez dwumian 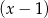 .
.
Wyznacz dziedzinę i najmniejszą wartość funkcji 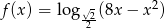 .
.
Wyznacz dziedzinę funkcji 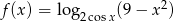 i zapisz ją w postaci sumy przedziałów liczbowych.
i zapisz ją w postaci sumy przedziałów liczbowych.
Funkcja 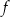 jest określona wzorem
jest określona wzorem
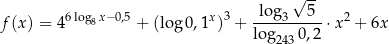
dla każdej liczby ![[ ] x ∈ 1,3 2](https://img.zadania.info/zad/5459831/HzadT2x.png) . Wyznacz zbiór wartości funkcji
. Wyznacz zbiór wartości funkcji 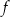 .
.
Wielomian 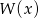 przy dzieleniu przez dwumiany
przy dzieleniu przez dwumiany 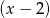 ,
, 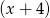 daje reszty odpowiednio równe -3 oraz -51. Wyznacz resztę z dzielenia wielomianu
daje reszty odpowiednio równe -3 oraz -51. Wyznacz resztę z dzielenia wielomianu 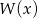 przez wielomian
przez wielomian 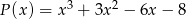 , wiedząc, że liczba -1 jest miejscem zerowym wielomianu
, wiedząc, że liczba -1 jest miejscem zerowym wielomianu 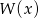 .
.
Wykaż, że jeżeli 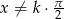 dla
dla 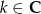 to prawdziwa jest tożsamość
to prawdziwa jest tożsamość
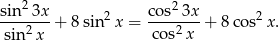
Jedynym miejscem zerowym funkcji kwadratowej 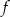 jest liczba 2. Wykres funkcji
jest liczba 2. Wykres funkcji 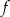 przecina oś
przecina oś 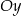 w punkcie o współrzędnych
w punkcie o współrzędnych 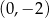 . Wyznacz wzór tej funkcji w postaci ogólnej.
. Wyznacz wzór tej funkcji w postaci ogólnej.
Funkcja kwadratowa 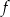 ma dokładnie jedno miejsce zerowe równe 2. Ponadto
ma dokładnie jedno miejsce zerowe równe 2. Ponadto 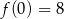 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 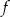 .
.
Wykaż, że funkcja 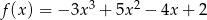 nie ma ekstremum.
nie ma ekstremum.
Wykaż, że 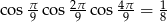 .
.
Funkcja kwadratowa 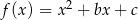 nie ma miejsc zerowych. Wykaż, że
nie ma miejsc zerowych. Wykaż, że 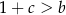 .
.
Wyznacz wszystkie wartości parametru 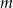 , dla których funkcja
, dla których funkcja 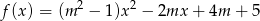 jest rosnąca w przedziale
jest rosnąca w przedziale 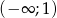 i malejąca w przedziale
i malejąca w przedziale 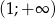 .
.
Wyznacz dziedzinę funkcji 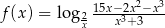
Funkcja 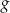 jest określona wzorem
jest określona wzorem 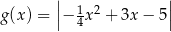 dla każdego
dla każdego 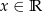 . Fragment wykresu funkcji
. Fragment wykresu funkcji 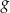 w kartezjańskim układzie współrzędnych
w kartezjańskim układzie współrzędnych 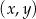 przedstawiono na rysunku (jednostki pominięto).
przedstawiono na rysunku (jednostki pominięto).
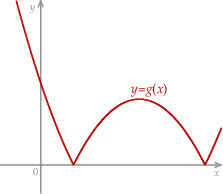
Wyznacz zbiór wszystkich wartości, jakie funkcja 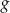 przyjmuje w przedziale
przyjmuje w przedziale ![[9,11]](https://img.zadania.info/zad/5661402/HzadT7x.gif) .
.
Funkcja 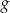 jest określona wzorem
jest określona wzorem 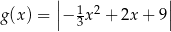 dla każdego
dla każdego 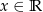 . Fragment wykresu funkcji
. Fragment wykresu funkcji 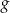 w kartezjańskim układzie współrzędnych
w kartezjańskim układzie współrzędnych 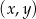 przedstawiono na rysunku (jednostki pominięto).
przedstawiono na rysunku (jednostki pominięto).
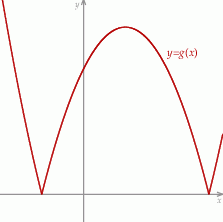
Wyznacz zbiór wszystkich wartości, jakie funkcja 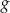 przyjmuje w przedziale
przyjmuje w przedziale ![[2,11]](https://img.zadania.info/zad/7071188/HzadT7x.gif) .
.
Wielomian 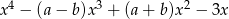 jest podzielny przez wielomian
jest podzielny przez wielomian 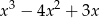 . Oblicz
. Oblicz  i
i 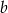 .
.
W poniższej tabeli podane są wartości funkcji kwadratowej 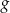 dla kilku wybranych argumentów zapisanych w kolejności rosnącej:
dla kilku wybranych argumentów zapisanych w kolejności rosnącej:
| x | -2 | -1 | 0 | 1 | |
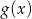 | -4 | 1 | 2 | -1 |
- Wyznacz wzór funkcji
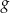 .
. - Uzupełnij brakujące zapisy w tabeli.
- Rozwiąż nierówność
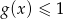 .
.
Przy dzieleniu wielomianu 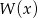 przez dwumian
przez dwumian 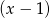 otrzymujemy iloraz
otrzymujemy iloraz 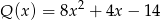 oraz resztę
oraz resztę 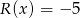 . Oblicz pierwiastki wielomianu
. Oblicz pierwiastki wielomianu 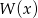 .
.
Funkcja homograficzna 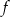 jest monotoniczna w przedziałach
jest monotoniczna w przedziałach 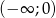 i
i 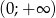 . Zbiór
. Zbiór 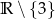 jest zbiorem wartości tej funkcji, a wartość 5 funkcja przyjmuje dla argumentu 3.
jest zbiorem wartości tej funkcji, a wartość 5 funkcja przyjmuje dla argumentu 3.
- Znajdź wzór funkcji
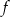 .
. - Wyznacz miejsce zerowe funkcji
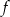 .
. - Wyznacz te argumenty, dla których funkcja
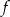 przyjmuje wartości większe od 1.
przyjmuje wartości większe od 1.
Dla jakich wartości parametru 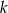 dziedziną funkcji
dziedziną funkcji 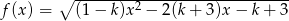 jest zbiór liczb rzeczywistych?
jest zbiór liczb rzeczywistych?
Reszta z dzielenia wielomianu 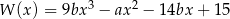 przez trójmian
przez trójmian 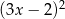 wynosi 3. Oblicz
wynosi 3. Oblicz  i
i 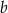 . Dla wyznaczonych wartości
. Dla wyznaczonych wartości  i
i 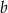 rozwiąż nierówność
rozwiąż nierówność 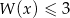 .
.

