Funkcja kwadratowa 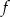 określona jest wzorem
określona jest wzorem 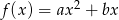 . Wiadomo, że
. Wiadomo, że 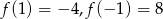 . Określ, dla jakich argumentów spełniona jest nierówność
. Określ, dla jakich argumentów spełniona jest nierówność 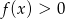 .
.
/Szkoła średnia/Funkcje
Wyznacz maksymalne przedziały monotoniczności funkcji 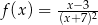 .
.
Wielomian 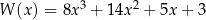 jest iloczynem wielomianów
jest iloczynem wielomianów 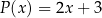 oraz
oraz 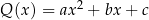 . Oblicz wartości współczynników:
. Oblicz wartości współczynników: 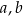 oraz
oraz  .
.
Kąt  jest ostry i
jest ostry i 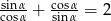 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 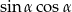 .
.
Kąt  jest ostry oraz
jest ostry oraz 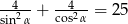 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 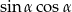 .
.
Funkcja 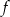 jest określona wzorem
jest określona wzorem
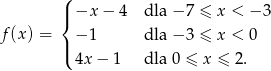
- Podaj dziedzinę funkcji
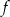 .
. - Podaj jej miejsca zerowe.
- Naszkicuj wykres tej funkcji.
- Podaj zbiór wartości funkcji
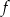 .
.
Oblicz wartość wyrażenia 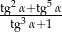 jeżeli
jeżeli 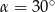 .
.
Z trzech prostopadłościennych belek 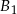 ,
, 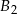 ,
, 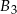 o takich samych przekrojach poprzecznych i długościach odpowiednio równych 1 m, 2 m, 1 m sklejono jedną belkę o długości 4 m. Każda z belek
o takich samych przekrojach poprzecznych i długościach odpowiednio równych 1 m, 2 m, 1 m sklejono jedną belkę o długości 4 m. Każda z belek 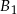 ,
, 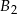 ,
,  wykonana jest z innego materiału, a ich masy są równe odpowiednio 20 kg, 30 kg, 10 kg.
wykonana jest z innego materiału, a ich masy są równe odpowiednio 20 kg, 30 kg, 10 kg.
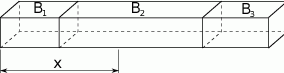
Masa odcinka belki o długosci  jest funkcją zmiennej
jest funkcją zmiennej  . Znajdź wzór tej funkcji.
. Znajdź wzór tej funkcji.
Wykaż, że
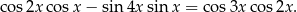
Wyznacz zbiór wartości funkcji 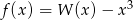 , gdzie
, gdzie 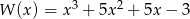 .
.
Dane są dwie funkcje kwadratowe 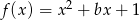 oraz
oraz 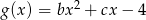 , gdzie
, gdzie 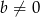 . Wyznacz wszystkie wartości parametrów
. Wyznacz wszystkie wartości parametrów 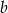 i
i  tak, aby funkcja
tak, aby funkcja 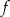 miała jedno miejsce zerowe i jednocześnie funkcja
miała jedno miejsce zerowe i jednocześnie funkcja 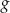 przyjmowała wartości ujemne dla każdego
przyjmowała wartości ujemne dla każdego 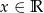 .
.
Wykaż, że nie istnieje kąt  , dla którego spełniona jest równość
, dla którego spełniona jest równość 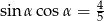 .
.
Funkcja liniowa 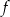 przyjmuje wartość 2 dla argumentu 0, a ponadto
przyjmuje wartość 2 dla argumentu 0, a ponadto 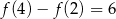 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 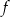 .
.
Funkcja liniowa 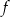 przyjmuje wartość 2 dla argumentu
przyjmuje wartość 2 dla argumentu 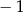 , a ponadto
, a ponadto 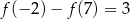 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 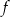 .
.
Wyznacz maksymalne przedziały monotoniczności funkcji 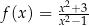 .
.
Funkcja 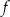 jest określona wzorem
jest określona wzorem 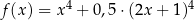 dla każdego
dla każdego 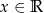 . Oblicz najmniejszą wartość tej funkcji.
. Oblicz najmniejszą wartość tej funkcji.
Wiedząc, że wielomian 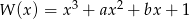 jest podzielny przez wielomian
jest podzielny przez wielomian 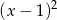 , oblicz
, oblicz  i
i 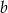 .
.
Dany jest wielomian 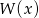 stopnia
stopnia 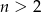 , którego suma wszystkich współczynników jest równa 4, a suma współczynników przy potęgach o wykładnikach nieparzystych jest równa sumie współczynników przy potęgach o wykładnikach parzystych. Wykaż, że reszta
, którego suma wszystkich współczynników jest równa 4, a suma współczynników przy potęgach o wykładnikach nieparzystych jest równa sumie współczynników przy potęgach o wykładnikach parzystych. Wykaż, że reszta 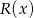 z dzielenia tego wielomianu przez wielomian
z dzielenia tego wielomianu przez wielomian 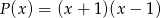 jest równa
jest równa 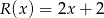 .
.
Wyznacz wzór ogólny funkcji kwadratowej, której największą wartością jest 2, a miejscami zerowymi są liczby 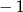 i 3.
i 3.
Wyznacz wzór ogólny funkcji kwadratowej, której najmniejszą wartością jest 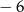 , a miejscami zerowymi są liczby
, a miejscami zerowymi są liczby 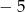 i 3.
i 3.
Wyznacz maksymalne przedziały monotoniczności funkcji 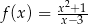 określonej dla
określonej dla 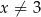 .
.
Wyznacz maksymalne przedziały monotoniczności funkcji 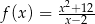 określonej dla
określonej dla 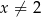 .
.
Wykaż, że jeżeli 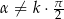 , gdzie
, gdzie 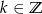 , to
, to
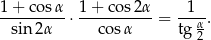
Funkcja 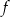 jest określona wzorem
jest określona wzorem 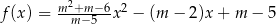 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz całkowite wartości parametru
. Wyznacz całkowite wartości parametru 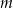 , dla których funkcja
, dla których funkcja 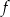 przyjmuje wartość największą i ma dwa różne miejsca zerowe o jednakowych znakach.
przyjmuje wartość największą i ma dwa różne miejsca zerowe o jednakowych znakach.
Funkcja kwadratowa 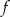 jest określona wzorem
jest określona wzorem 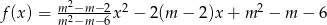 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 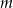 , dla których rozwiązaniem nierówności
, dla których rozwiązaniem nierówności 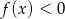 jest przedział postaci
jest przedział postaci 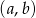 , gdzie
, gdzie 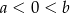 .
.
Funkcja 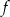 jest określona wzorem
jest określona wzorem 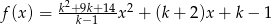 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz całkowite wartości parametru
. Wyznacz całkowite wartości parametru 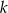 , dla których funkcja
, dla których funkcja 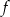 przyjmuje wartość największą i ma dwa różne miejsca zerowe o jednakowych znakach.
przyjmuje wartość największą i ma dwa różne miejsca zerowe o jednakowych znakach.

