Reszta z dzielenia wielomianu 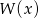 przez wielomian
przez wielomian 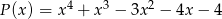 jest wielomianem
jest wielomianem 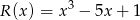 . Wyznacz resztę z dzielenia tego wielomianu przez wielomian
. Wyznacz resztę z dzielenia tego wielomianu przez wielomian 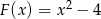 .
.
/Szkoła średnia/Funkcje
Dana jest funkcja 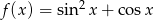 dla
dla 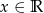 .
.
- Rozwiąż równanie
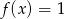 w przedziale
w przedziale 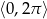 .
. - Wyznacz największą wartość funkcji
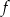 .
.
Reszta z dzielenia wielomianu 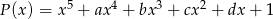 przez dwumian
przez dwumian 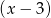 jest równa 1. Wykaż, że jeżeli liczby
jest równa 1. Wykaż, że jeżeli liczby 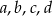 są liczbami całkowitymi to wielomian
są liczbami całkowitymi to wielomian 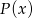 nie ma pierwiastków wymiernych.
nie ma pierwiastków wymiernych.
Przedstaw wielomian 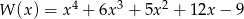 w postaci iloczynu dwóch wielomianów stopnia drugiego o współczynnikach całkowitych i tak, aby współczynniki przy drugich potęgach były równe jeden.
w postaci iloczynu dwóch wielomianów stopnia drugiego o współczynnikach całkowitych i tak, aby współczynniki przy drugich potęgach były równe jeden.
Oblicz wartość wyrażenia 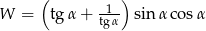 .
.
Oblicz wartość wyrażenia 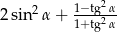 , gdzie
, gdzie  jest kątem ostrym.
jest kątem ostrym.
Podaj wartość wyrażenia 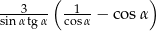 dla
dla 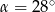 nie używając tablic.
nie używając tablic.
Wyznacz dziedzinę funkcji 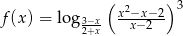
Wyznacz dziedzinę funkcji 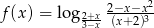 .
.
Reszty z dzielenia wielomianu 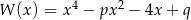 przez dwumiany
przez dwumiany 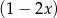 i
i 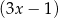 są odpowiednio równe
są odpowiednio równe 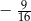 i
i 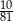 . Oblicz resztę z dzielenia wielomianu
. Oblicz resztę z dzielenia wielomianu 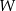 przez dwumian
przez dwumian 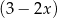 .
.
Wielomiany 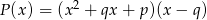 i
i 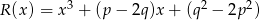 są równe. Oblicz
są równe. Oblicz 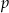 i
i 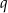 .
.
Wyznacz wszystkie wartości parametru 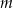 , dla których funkcja
, dla których funkcja 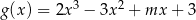 ma ekstremum lokalne równe 10.
ma ekstremum lokalne równe 10.
Dany jest wielomian 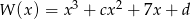 .
.
- Wyznacz wartości współczynników
 i
i 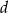 wielomianu
wielomianu 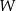 , wiedząc, że jest podzielny przez dwumian
, wiedząc, że jest podzielny przez dwumian 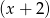 , zaś przy dzieleniu przez dwumian
, zaś przy dzieleniu przez dwumian 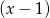 otrzymujemy resztę 3.
otrzymujemy resztę 3. - Dla
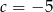 i
i 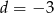 rozwiąż nierówność
rozwiąż nierówność 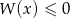 .
.
Wyznacz te wartości parametru 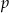 , dla których dziedziną funkcji
, dla których dziedziną funkcji 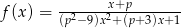 jest zbiór liczb rzeczywistych.
jest zbiór liczb rzeczywistych.
Sprawdź, czy prawdziwa jest następująca tożsamość 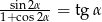 . Podaj konieczne założenia.
. Podaj konieczne założenia.
Sprawdź, czy prawdziwa jest następująca tożsamość 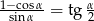 . Podaj konieczne założenia.
. Podaj konieczne założenia.
Sprawdź, czy prawdziwa jest tożsamość 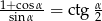 . Podaj konieczne założenia.
. Podaj konieczne założenia.
Wykaż, że jeżeli wielomian 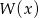 jest podzielny przez
jest podzielny przez 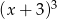 , to wielomian
, to wielomian 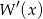 jest podzielny przez
jest podzielny przez 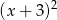 .
.
Wiadomo, że funkcja liniowa 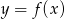 przyjmuje wartości dodatnie wtedy i tylko wtedy, gdy
przyjmuje wartości dodatnie wtedy i tylko wtedy, gdy 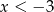 . Ponadto,
. Ponadto, 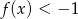 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 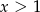 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 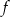 .
.
Funkcja kwadratowa 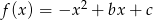 ma dwa miejsca zerowe:
ma dwa miejsca zerowe: 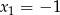 i
i 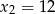 . Oblicz największą wartość tej funkcji.
. Oblicz największą wartość tej funkcji.
Funkcja kwadratowa 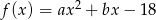 ma dwa miejsca zerowe:
ma dwa miejsca zerowe: 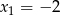 i
i 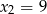 . Oblicz najmniejszą wartość tej funkcji.
. Oblicz najmniejszą wartość tej funkcji.
Kąta  jest ostry oraz
jest ostry oraz 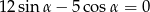 . Oblicz
. Oblicz 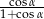 .
.
Wykaż, że
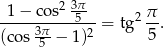
Dla jakich wartości parametru  reszta z dzielenia wielomianu
reszta z dzielenia wielomianu 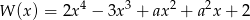 przez dwumian
przez dwumian 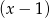 jest większa od 3.
jest większa od 3.
Wyznacz najmniejszą wartość funkcji kwadratowej 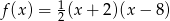 w przedziale
w przedziale 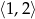 .
.
Wyznacz najmniejszą wartość funkcji 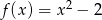 w przedziale
w przedziale 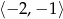 .
.
Funkcja kwadratowa jest określona wzorem 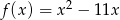 . Oblicz najmniejszą wartość funkcji
. Oblicz najmniejszą wartość funkcji 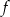 w przedziale
w przedziale 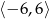 .
.
Funkcja kwadratowa jest określona wzorem 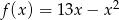 . Oblicz największą wartość funkcji
. Oblicz największą wartość funkcji 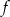 w przedziale
w przedziale 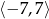 .
.
Uzasadnij, że dla każdej liczby naturalnej  wartość wielomianu
wartość wielomianu 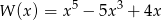 jest liczbą podzielną przez 120.
jest liczbą podzielną przez 120.

