Wyznacz wszystkie wartości parametru 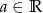 , dla których funkcja
, dla których funkcja 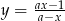 jest rosnąca w każdym przedziale, na którym jest określona. Dla
jest rosnąca w każdym przedziale, na którym jest określona. Dla 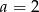 wyznacz zbiór wartości funkcji.
wyznacz zbiór wartości funkcji.
/Szkoła średnia/Funkcje
Kąt  jest ostry i
jest ostry i 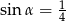 . Oblicz
. Oblicz 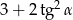 .
.
Kąt  jest ostry i
jest ostry i 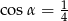 . Oblicz
. Oblicz 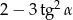 .
.
Kąt  jest ostry i
jest ostry i 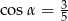 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia
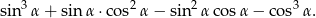
Kąt  jest ostry i
jest ostry i 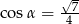 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 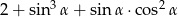 .
.
Kąt  jest ostry oraz
jest ostry oraz 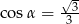 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 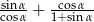 .
.
Kąt  jest ostry
jest ostry 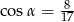 . Oblicz
. Oblicz 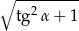 .
.
Kąt  jest ostry i
jest ostry i 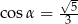 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 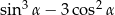 .
.
Kąt  jest ostry i
jest ostry i 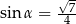 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 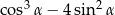 .
.
Reszta z dzielenia wielomianu 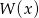 przez wielomian
przez wielomian 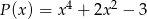 jest wielomianem
jest wielomianem 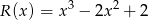 . Wyznacz resztę z dzielenia tego wielomianu przez wielomian
. Wyznacz resztę z dzielenia tego wielomianu przez wielomian 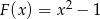 .
.
Wynikiem dzielenia wielomianu 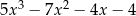 przez dwumian
przez dwumian 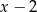 jest trójmian kwadratowy postaci
jest trójmian kwadratowy postaci 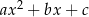 . Oblicz
. Oblicz 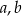 i
i  .
.
Wynikiem dzielenia wielomianu 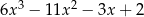 przez dwumian
przez dwumian 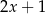 jest trójmian kwadratowy postaci
jest trójmian kwadratowy postaci 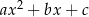 . Oblicz
. Oblicz 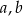 i
i  .
.
W wyniku podzielenia wielomianu 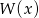 przez
przez 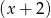 otrzymujemy iloraz
otrzymujemy iloraz 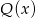 i resztę 0. Jeśli natomiast podzielimy wielomian
i resztę 0. Jeśli natomiast podzielimy wielomian 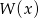 przez
przez 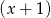 , to otrzymamy iloraz
, to otrzymamy iloraz 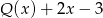 i resztę 2.
i resztę 2.
- Wyznacz wielomian
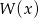 .
. - Rozwiąż nierówność
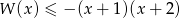 .
.
Wielomian 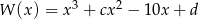 jest podzielny przez dwumian
jest podzielny przez dwumian 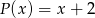 . Przy dzieleniu wielomianu
. Przy dzieleniu wielomianu 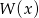 przez dwumian
przez dwumian 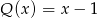 otrzymujemy resztę
otrzymujemy resztę 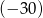 . Oblicz pierwiastki wielomianu
. Oblicz pierwiastki wielomianu 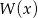 i rozwiąż nierówność
i rozwiąż nierówność 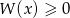 .
.
Wielomian 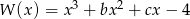 jest podzielny przez trójmian kwadratowy
jest podzielny przez trójmian kwadratowy 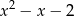 . Wyznacz współczynniki
. Wyznacz współczynniki 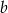 i
i  wielomianu
wielomianu 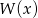 .
.
Wielomian 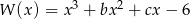 jest podzielny przez trójmian kwadratowy
jest podzielny przez trójmian kwadratowy 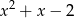 . Wyznacz współczynniki
. Wyznacz współczynniki 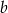 i
i  wielomianu
wielomianu 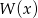 .
.
Wyznacz wzór funkcji liniowej 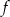 , wiedząc że nie przyjmuje ona wartości dodatnich oraz
, wiedząc że nie przyjmuje ona wartości dodatnich oraz 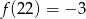 .
.
Oblicz granicę 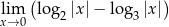 .
.
Dany jest wielomian 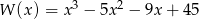 .
.
- Sprawdź, czy punkt
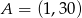 należy do wykresu tego wielomianu.
należy do wykresu tego wielomianu. - Zapisz wielomian
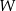 w postaci iloczynu trzech wielomianów stopnia pierwszego.
w postaci iloczynu trzech wielomianów stopnia pierwszego.
Dla jakiej wartości parametru 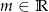 funkcja
funkcja 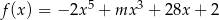 ma ekstremum w punkcie
ma ekstremum w punkcie 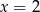 ?
?
Dany jest wielomian 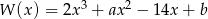 .
.
- Dla
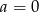 i
i 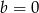 otrzymamy wielomian
otrzymamy wielomian 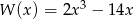 . Rozwiąż równanie
. Rozwiąż równanie 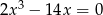 .
. - Dobierz wartości
 i
i 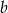 tak, aby wielomian
tak, aby wielomian 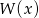 był podzielny jednocześnie przez
był podzielny jednocześnie przez 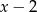 oraz
oraz 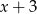 .
.
Funkcję kwadratową 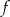 można opisać wzorem mającym postać
można opisać wzorem mającym postać 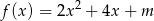 .
.
- Wyznacz warunek, dla którego funkcja
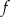 ma dwa różne pierwiastki
ma dwa różne pierwiastki 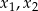 , a następnie oblicz
, a następnie oblicz 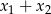 .
. - Wiedząc dodatkowo, że
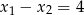 , oblicz
, oblicz 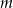 . Dla wyznaczonej liczby
. Dla wyznaczonej liczby 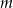 naszkicuj wykres funkcji
naszkicuj wykres funkcji 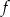 w układzie współrzędnych, a następnie rozwiąż równanie
w układzie współrzędnych, a następnie rozwiąż równanie 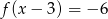 .
. 
Funkcja kwadratowa 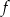 ma następujące własności:
ma następujące własności:
– zbiorem wartości funkcji 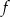 jest przedział
jest przedział 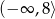 ;
;
– funkcja 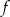 jest rosnąca w przedziale
jest rosnąca w przedziale 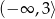 i malejąca w przedziale
i malejąca w przedziale 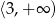 ;
;
– wykres funkcji 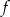 przecina oś
przecina oś 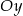 w punkcie, którego rzędna jest równa
w punkcie, którego rzędna jest równa 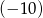 .
.
Wyznacz wzór funkcji 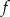 w postaci iloczynowej.
w postaci iloczynowej.
Dla jakich wartości parametru 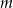 funkcja
funkcja
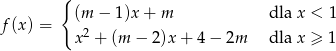
przyjmuje tylko dodatnie wartości?
Oblicz 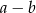 , gdy
, gdy 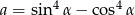 ,
, 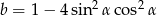 dla
dla 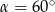 .
.
Wyznacz dziedzinę funkcji 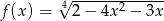 .
.
Wyznacz dziedzinę funkcji 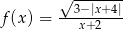 .
.
Wyznacz dziedzinę funkcji 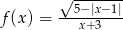 .
.
Wiedząc, że  jest kątem ostrym oraz
jest kątem ostrym oraz 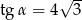 oblicz wartość wyrażenia
oblicz wartość wyrażenia 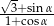 .
.
Wiedząc, że  jest kątem ostrym i
jest kątem ostrym i 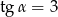 , oblicz wartość wyrażenia
, oblicz wartość wyrażenia 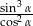 .
.
Kąt  jest kątem ostrym i
jest kątem ostrym i 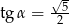 . Oblicz
. Oblicz 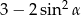 .
.
Wiedząc, że  jest kątem ostrym i
jest kątem ostrym i 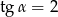 , oblicz wartość wyrażenia
, oblicz wartość wyrażenia 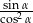 .
.
Kąt  jest ostry i
jest ostry i 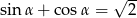 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 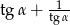 .
.
Kąt  jest ostry i
jest ostry i  . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 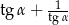 .
.

