/Szkoła średnia/Funkcje

Zadanie nr 1362758

Dana jest funkcja kwadratowa 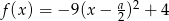a 2 f(x) = − 9(x − 2) + 4

  • Dla 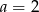a = 2 wyznacz postać iloczynową tej funkcji.
  • Dla 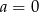a = 0 wyznacz te argumenty, dla których funkcja osiąga wartości ujemne.
  • Wyznacz a tak, aby osią symetrii wykresu funkcji była prosta o równaniu x = 6 .
Wersja PDF

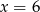Rozwiązanie

  • Liczymy
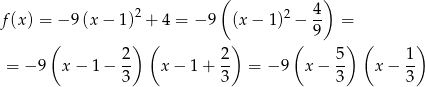
    ( ) 2 2 4- f(x ) = − 9(x − 1) + 4 = −9 (x− 1) − 9 = ( ) ( ) ( ) ( ) = − 9 x− 1− 2- x − 1 + 2- = − 9 x− 5- x − 1- 3 3 3 3

     
    Odpowiedź: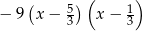 ( 5)( 1) − 9 x − 3 x− 3

  • Musimy rozwiązać nierówność
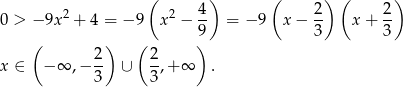
    ( 4) ( 2) ( 2 ) 0 > − 9x2 + 4 = −9 x2 − -- = − 9 x − -- x + -- ( ) ( 9) 3 3 2- 2- x ∈ − ∞ ,− 3 ∪ 3 ,+ ∞ .

     
    Odpowiedź: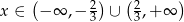 x ∈ (− ∞ ,− 2) ∪ (2,+ ∞ ) 3 3

  • Osią symetrii wykresu funkcji kwadratowej jest zawsze prosta 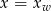x = xw przechodząca przez wierzchołek paraboli. Daje to nam równanie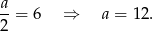
    a- 2 = 6 ⇒ a = 12 .

     
    Odpowiedź: a = 12

Wersja PDF