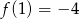Zadanie nr 4026126
Oblicz najmniejszą wartość funkcji kwadratowej 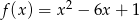 w przedziale
w przedziale 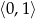 .
.
Rozwiązanie
Pierwsza współrzędna wierzchołka paraboli będącej wykresem funkcji 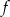 jest równa
jest równa
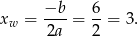
Ponieważ punkt ten jest na prawo od podanego przedziału, funkcja jest malejąca na tym przedziale (bo ramiona paraboli są skierowane do góry), czyli wartość najmniejszą jest osiągana w prawym końcu przedziału i wynosi
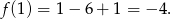
Dla ciekawskich obrazek.
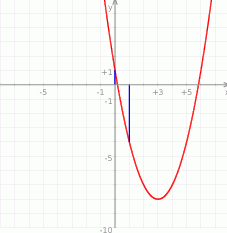
Odpowiedź: