/Szkoła średnia/Funkcje

Zadanie nr 4912838

Dodaj do ulubionych
Dodaj do rozwiązanych

Dana jest funkcja 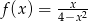--x- f(x ) = 4−x2 , gdzie 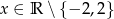x ∈ R ∖ {− 2,2} . Wykaż, że zbiorem wartości tej funkcji jest zbiór liczb rzeczywistych.

Rozwiązanie

Musimy wykazać, że równanie (z niewiadomą x )

f(x ) = m

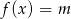
ma rozwiązanie dla dowolnego 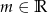m ∈ R . Liczymy

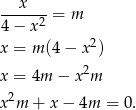
x -----2-= m 4− x x = m (4− x2) 2 x = 4m − x m x2m + x − 4m = 0.

Jeżeli 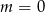m = 0 , to równanie to ma rozwiązanie 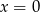x = 0 . Jeżeli natomiast 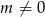m ⁄= 0 , to jest to zwykłe równanie kwadratowe z parametrem. Ponieważ 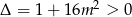2 Δ = 1 + 16m > 0 , to równanie to ma zawsze dwa rozwiązania.

Nie jest to jednak jeszcze koniec – musimy sprawdzić, że te rozwiązania to nie jest para 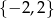{− 2,2} . To jednak łatwo wynika ze wzorów Viète’a:

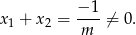
−-1- x1 + x2 = m ⁄= 0.

Tak więc zbiorem rozwiązań tego równania nie może być para 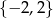{ −2 ,2} , co pokazuje, że każda liczba rzeczywista jest wartością danej funkcji.

Wersja PDF